Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) chỉ dùng R1 ta có \(Q=k.\dfrac{U^2}{R1}.t1\) (1)
Chỉ dùng R2 => \(Q=k.\dfrac{U^2}{R2}.10\) (2)
Lấy 1:2 => \(1=\dfrac{R2.t1}{10.R1}=>t1=\dfrac{20}{3}phút\)
b) R1ntR2=>Q=\(k.\dfrac{U^2}{R1+R2}.tnt=\dfrac{U^2}{20}.k.tnt\) (3)
Lấy 2:3=>\(1=\dfrac{20.10}{tnt.R2}=>tnt=\dfrac{50}{3}phút\)
c) mắc R1//R2=>\(Q=k.\dfrac{U^2}{\dfrac{8.12}{8+12}}.tss\) (4)
Lấy 2:4=>\(1=\dfrac{10.24}{tss.5.12}=>tss=4\) phút
Vậy.......

1. a. Theo ht 4' trg đm //, ta có: Rtđ= (R1.R2)/(R1+R2)= (3.6)/(3+6)=2 ôm
b.Theo ĐL ôm, ta có: I= U/Rtđ=24/2=12 A
I1=U/R1=24/3=8 ôm
I2=U/R2=24/6=4 ôm
2. a. Theo ht 4' trg đm //, ta có: Rtđ=(R1.R2.R3)/(R1+R2+R3)= (6.12.4)/(6+12+4)=13,09 ôm
b. Áp dụng ĐL Ôm, ta có: U=I.R=3.13,09=39,27 V
c. Theo ĐL Ôm, ta có:
I1=U/R1=39,27/6=6.545 A
I2=U/R2=39,27/12=3,2725 A
I3=U/R3=39,27/4=9.8175 A

a. Điện trở tương đương của mạch là: R t đ = R 1 + R 2 = 40
Cường độ dòng điện qua mỗi điện trở là:
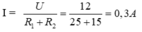
b. Đổi S = 0 , 06 m m 2 = 0 , 06 . 10 - 6 m 2
Công thức tính điện trở:
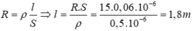
c. Cường độ dòng điện định mức của đèn:
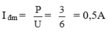
Vì đèn sáng bình thường nên hiệu điện thế giữa hai đầu R 1 là 6V
Vậy hiệu điện thế hai đầu biến trở là: U b = U - U đ = 12 - 6 = 6 V
ường điện dòng điện chạy qua R 1 là: I 1 = 6 / 25 = 0 , 24 A
Cường điện dòng điện chạy qua biến trở là: I b = I 1 + I đ m = 0 , 74 A
Vậy điện trở biến trở khi đó là:
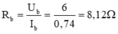

Điện trở tương đương
\(R_{tđ}=R_1+R_2=12+20=32\left(\Omega\right)\)
Cường độ dòng điện toàn mạch
\(I=\dfrac{U}{R_{tđ}}=\dfrac{20}{32}=0,625\left(A\right)\)
Chúc bạn học tốt

Điện trở tương đương: \(R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}=6\left(\Omega\right)\)
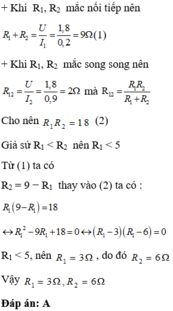
a. Mạch gồm: R1 nt R2
- Vì R1 nt R2 => Điện trở tương đương Rtđ = R1 + R2 = 90 (\(\Omega\))
- Áp dụng định luật Ôm => Cường độ dòng điện của mỗi điện trở bằng CĐDĐ chạy qua mạch chính
I1 = I2 = Im = \(\dfrac{U_m}{R_{tđ}}\) = \(\dfrac{30}{90}\) = \(\dfrac{1}{3}\) (A)
b.
- Khi dùng riêng dây 1 : \(P_1=\dfrac{U^2}{R_1}\) => t1 = \(\dfrac{Q}{\dfrac{U^2}{R^{_1}}}\) = \(\dfrac{Q}{U^2}.R_1\)
- Khi dùng riêng dây 2 : t2 = \(\dfrac{Q}{U^2}.R_2\)
R1 nt R2 => \(P=\dfrac{U^2}{R_1+R_2}\) => t3 = \(\dfrac{Q}{U^2}.\left(R_1+R_2\right)\)=t1+t2= 10'
R1 // R2 => \(P=\dfrac{U^2}{\dfrac{R_1.R_2}{R_1+R_2}}\) => t4 = \(\dfrac{Q}{U^2}.\dfrac{R_1.R_2}{R_1+R_2}\)
=> \(\dfrac{1}{t_4}=\dfrac{1}{t_1}+\dfrac{1}{t_2}\) => t4 = ...