Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
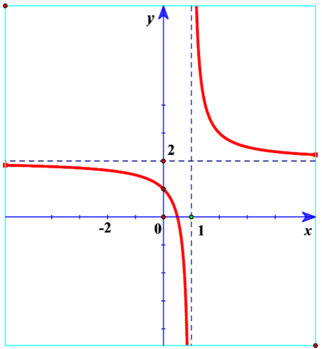
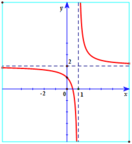
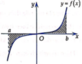
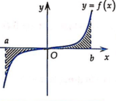
Dựa vào đồ thị, ta có tiệm cận đứng x = 1, tiệm cận ngang y = 2 và đồ thị đi qua điểm (0; 1) nên
![]()
![]()
Đồ thị hàm số y = a x - 1 b x + c có tiệm cận đứng x = 1 b , tiệm cân ngang y = a b 2
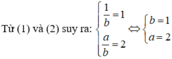

Chọn D.
Dựa vào đồ thị, ta có tiệm cận đứng x = 1 , tiệm cận ngang y = 2 và đồ thị đi qua điểm 0 ; 1 (1). Đồ thị hàm số y = a x - 1 b x + c có tiệm cận đứng x = - c b , tiệm cận ngang y = a và đi qua điểm 0 ; - 1 b (2). Từ (1) và (2) suy ra: a = 2 , b = 1 , c = - 1 .

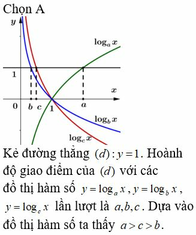
Đáp án D
Cách giải:
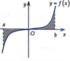
Ta thấy, hai hàm số y = logax, y = logbx đều đồng biến trên (0;+∞) ⇒ a, b > 1
Lấy x0 > 0 bất kì, ta thấy logax0 > logbx0 ⇒ a < b ⇒ 1 < a < b
Hàm số y = cx nghịch biến trên R ⇒ c < 1 ⇒ c < a < b

Đáp án C
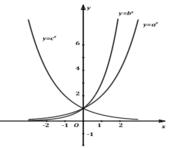
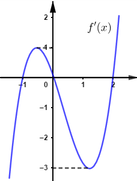
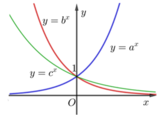
Dựa vào hình vẽ, ta thấy rằng:
Hàm số y = ax là hàm số đồng biến; hàm số y = bx, y = cx là hàm số nghịch biến.
Suy ra a > 1 và 0 < b < 1 0 < c < 1 → a > b ; c
Gọi B(-1; yB) thuộc đồ thị hàm số y = b x ⇒ y B = 1 b
Và C(-1;yc) thuộc đồ thị hàm số y = c x ⇒ y C = 1 c
Dựa vào đồ thị, ta có y B > y c ⇒ 1 b > 1 c ⇒ c > b
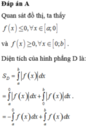

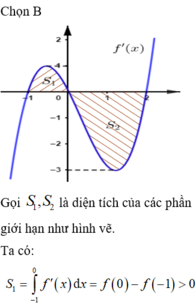
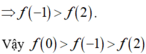
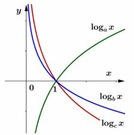

Chọn C
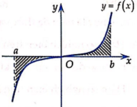
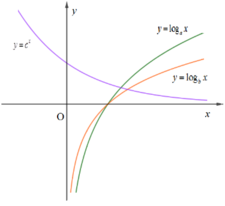
Đồ thị hàm số y = a x , y = b x là đồ thị của hàm số mũ cơ bản đồng biến nên a > 1; b > 1
Dựa vào đồ thị ta có :
Do đó: b > a > 1
Đồ thị hàm số y = c x là đồ thị của hàm số mũ cơ bản nghịch biến nên 0 < c < 1
Vậy b > a > c