Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOD.
Kết luận: OE ⊥ OF
Chọn đáp án A.

Đáp án C
Giả thiết: Cho góc bẹt AOB và tia OD. OE là phân giác góc BOD; OF là phân giác góc AOD.
Kết luận: OE⊥OF

O x y z m m 1 2 3 4
Cho 2 góc xOy và yOz kề bù .
Om ; On lần lượt là tia phân giác của 2 góc đó
\(\Rightarrow\begin{cases}\widehat{O_1}=\widehat{O_2}=\frac{1}{2}.\widehat{xOy}\\\widehat{O_3}=\widehat{O_4}=\frac{1}{2}.\widehat{yOz}\end{cases}\)
\(\Rightarrow\widehat{O_2}+\widehat{O_3}=\frac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)=\frac{1}{2}.180^0=90^0\)
=> Đpcm
* Vẽ hình: Vẽ hình hơi xấu chút! ![]()
x y O z t t'
* Viết giả thiết, kết luận:
GT: - Góc xOz và góc yOz là hai góc kề bù
- Ot là tia phân giác của góc xOz
- Ot' là tia phân giác của góc yOz
KL: Góc tot' là 1 góc vuông
* Chứng minh:
Góc xOt = góc tOz = 1/2 . góc xOz (vì Ot là tia phân giác của góc xOz)
Góc yot' = góc t'Oz = 1/2 . góc yOz (vì Ot' là tia phân giác của góc yOz)
Góc xOz + góc yOz = 180 độ (vì 2 góc kề bù)
Vì góc xOz và góc yOz là 2 góc kề bù mà
Ot là tia phân giác xOz
Ot' là tia phân giác yOz
=> Tia Oz nằm giữa hai tia Ot và Ot' nên:
Góc tOt' = góc tOz + góc t'Oz = 1/2 . góc xOz + 1/2 . góc yOz = 1/2 . (góc xOz + góc yOz) = 1/2 . 180 độ = 90 độ
Vậy tOt' là 1 góc vuông.
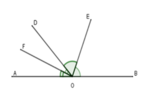

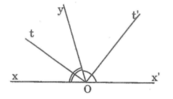
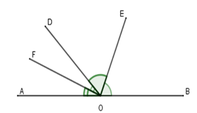
Giả thiết là hai tia phân giác của hai góc kề bù
Kết luận là hai tia đó tạo thành một góc vuông