Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
hay BMNC là hình thang
b: Xét ΔABK có MI//BK
nên MI/BK=AM/AB=1/2(1)
XétΔACK có NI//CK
nên NI/CK=AN/AC=1/2(2)
Từ (1)và (2) suy ra MI/BK=NI/CK
mà MI=NI
nên BK=CK
hay K là trug điểm của BC
Xét ΔABC có
K là trung điểm của BC
M là trung điểm của AB
Do đó: KM là đường trung bình
=>KM//AN và KM=AN
hay AMKN là hình bình hành
a: Xét ΔHAB có
M là trung điểm của HA
N là trung điểm của HB
Do đó: MN là đường trung bình
=>MN//AB
hay ABNM là hình thang
a: Xét tứ giác AEMF có
AE//MF
AF//ME
Do đó: AEMF là hình bình hành
Hình bình hành AEMF có \(\widehat{FAE}=90^0\)
nên AEMF là hình chữ nhật
b: Xét ΔABC có
E là trung điểm của BA
EM//AC
Do đó: M là trung điểm của BC
Xét ΔABC có
M là trung điểm của BC
MF//AB
Do đó: F là trung điểm của AC
Xét ΔABC có
E,F lần lượt là trung điểm của AB,AC
=>EF là đường trung bình
=>EF//BC
=>EF//MH
ΔHAC vuông tại H
mà HF là đường trung tuyến
nên \(HF=AF\)
mà AF=ME(AEMF là hình chữ nhật)
nên ME=FH
Xét tứ giác MHEF có MH//EF
nên MHEFlà hình thang
mà ME=FH
nên MHEF là hình thang cân
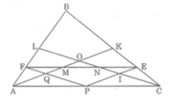
Gọi Q là giao điểm của PF và AK ,I là giao điểm của PE và CL
Trong △ FPE ta có: PE//AK hay QM //PE
Suy ra: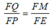 
(định lí ta-lét) (1)
Trong △ ALO ta có:PF //CL hay FQ //LO
Suy ra: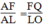
(định lí ta-lét) (2)
Trong △ ALC ta có: PF // CL
Suy ra: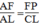 
(định lí ta-lét) (3)
Từ (2) và (3) suy ra: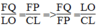 
Vì LO = 1/3 CL (O giao điểm của hai đường trung tuyến) nên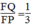 
(4)
Từ (1) và (4) suy ra: 
⇒ FM = 1/3 FE
Trong △ EPF ta có:PF // CL hay NI // PF
Suy ra: 
(định lí ta –lét) (5)
Trong △ CKO ta có: EI // OK
Suy ra: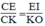 
(định lí ta –lét) (6)
Trong △ CKA ta có:PE // AK
Suy ra: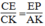 
(định lí ta –lét) (7)
Từ (6) và (7) suy ra: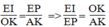 
Vì OK = 1/3 AK (O là giao điểm của hai đường trung tuyến) nên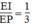 
(8)
Từ (5) và (8) suy ra: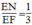 
⇒EN = 1/3 EF
Ta có: MN = EF - (EN + FM) = EF - (1/3 EF + 1/3 EF) = 1/3 EF
Vậy EN = MN = NF
Gọi J là giao điểm của BP và KE; Xét \(\Delta\)BSJ có:
PE // BS; PE = \(\dfrac{1}{2}\) BS
⇒ PF là đường trung bình của \(\Delta\)BSJ (vì đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy)
⇒ PJ = PB; EJ = ES (1)
Xét \(\Delta\)ABJ có: AF = FB (gt); PJ = PB theo (1)
⇒ PF là đường trung bình của \(\Delta\) ABJ (vì đường trung bình của tam giác đi qua trung điểm hai cạnh của tam giác và song song với cạnh còn lại)
⇒ PF// AJ (2)
Xét tứ giác ASCJ ta có: E là giao điểm hai đường chéo
AE = EC (gt)
EJ = ES ( theo (1)
⇒ Tứ giác ASCJ là hình bình hành vì tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
⇒ CS // CJ (3)
Kết hợp (2) và(3) ta có:
CS // PF ( vì trong cùng một mặt phẳng hai đường thẳng cùng song song với đường thẳng thứ ba thì song song với nhau.)
Kết luận: nếu BS = 2EP thì CS // PF điều phải chứng minh