Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

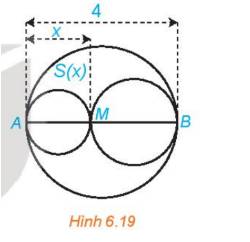
Ta có: AM<AB nên \(0 < x < 4\)
Diện tích hình tròn đường kính AB là \({S_0} = \pi .{\left( {\frac{{AB}}{2}} \right)^2} = 4\pi \)
Diện tích hình tròn đường kính AM là \({S_1} = \pi .{\left( {\frac{{AM}}{2}} \right)^2} = \frac{{\pi .{x^2}}}{4}\)
Diện tích hình tròn đường kính MB là \({S_2} = \pi .{\left( {\frac{{MB}}{2}} \right)^2} = \pi .\frac{{{{\left( {4 - x} \right)}^2}}}{4}\)
Diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ là \(S(x) = {S_0} - {S_1} - {S_2} = 4\pi - \frac{{{x^2}}}{4}\pi - \frac{{{{\left( {4 - x} \right)}^2}}}{4}\pi = \frac{{ - {x^2} + 4x}}{2}\pi \)
Vì diện tich S(x) không vượt quá 1 nửa tổng diện tích hai hình tròn nhỏ nên:
\(S(x) \le \frac{1}{2}\left( {{S_1} + {S_2}} \right)\)
Khi đó : \(\frac{{ - {x^2} + 4x}}{2}\pi \le \frac{1}{2}.\frac{{{x^2} - 4x + 8}}{2}\pi \)
\( \Leftrightarrow - {x^2} + 4x \le \frac{{{x^2} - 4x + 8}}{2}\)
\( \Leftrightarrow - 2{x^2} + 8x \le {x^2} - 4x + 8\)
\( \Leftrightarrow 3{x^2} - 12x + 8 \ge 0\)
Xét tam thức \(3{x^2} - 12x + 8\) có \(\Delta ' = 12 > 0\) nên f(x) có 2 nghiệm phân biệt \({x_1} = \frac{{6 - 2\sqrt 3 }}{3};{x_2} = \frac{{6 + 2\sqrt 3 }}{3}\)
Mặt khác a=3>0, do đó ta có bảng xét dấu:
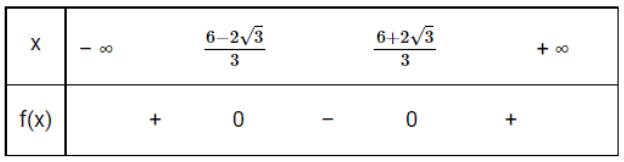
Do đó \(f(x) \ge 0\) với mọi \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\)
Mà 0<x<4 nên \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\)

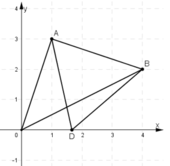
a) D nằm trên trục Ox nên D có tọa độ D(x ; 0)
Khi đó :
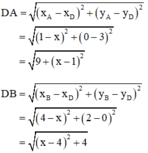
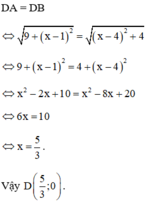
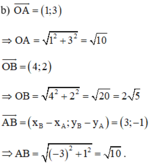
Vậy chu vi tam giác OAB là P = AO + BO + AB = √10 + 2√5 + √10 = 2√5 + 2√10
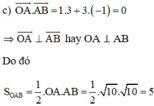

a) D nằm trên trục Ox nên tọa độ của D là (x; 0).
Ta có :
DA2 = (1 – x)2 + 32
DB2 = (4 – x)2 + 22
DA = DB => DA2 = DB2
<=> (1 – x)2 + 9 = (4 – x)2 + 4
<=> 6x = 10
=> x = => D(
; 0)

b)
OA2 = 12 + 32 =10 => OA = √10
OB2 = 42 + 22 =20 => OA = √20
AB2 = (4 – 1)2 + (2 – 3)2 = 10 => AB = √10
Chu vi tam giác OAB: √10 + √10 + √20 = (2 + √2)√10.
c) Ta có = (1; 3)
= (3; -1)
1.3 + 3.(-1) = 0 => .
= 0 =>
⊥
SOAB = |
| .|
| => SOAB =5 (dvdt)

Giải:
a) D nằm trên trục \(Ox\) nên tọa độ của D là \((x; 0).\)
Ta có :
\(DA^2 = (1 - x)^2+ 3^2\)
\(DB^2 = (4 - x)^2+ 2^2\)
\(DA = DB \)
\(\Rightarrow DA^2 = DB^2\)
\(\Leftrightarrow(1-x)^2+9=(4-x)^2+4\)
\(\Leftrightarrow6x = 10\)
\(\Rightarrow x=\dfrac{5}{3}\)
\(\Rightarrow D\)\(\left(\dfrac{5}{3};0\right)\)
b) Ta có:
\(\overrightarrow{OA}= (1; 3)\)
\(\overrightarrow{AP}=\left(3;-1\right)\)
\(1.3 + 3.(-1) = 0 \)
\(\Rightarrow\overrightarrow{OA}=\overrightarrow{OB}=0\)
\(\Rightarrow\overrightarrow{OA}\perp\overrightarrow{AB}\)
SOAB = |
| .|
| => SOAB =5 (dvdt)
a) D nằm trên trục Ox nên tọa độ của D là (x; 0).
Ta có :
DA2 = (1 - x)2 + 32
DB2 = (4 - x)2 + 22
DA = DB => DA2 = DB2
<=> (1 - x)2 + 9 = (4 - x)2 + 4
<=> 6x = 10
=> x = => D(
; 0)
c) Ta có = (1; 3)
= (3; -1)
1.3 + 3.(-1) = 0 => .
= 0 =>
⊥
SOAB = |
| .|
| => SOAB =5 (dvdt)

Gọi \(M\left(m^2;m\right)\) với \(-1< m< 3\)
\(\Rightarrow S_{MAB}=\dfrac{1}{2}\left|\left(x_M-x_A\right)\left(y_B-y_A\right)-\left(x_B-x_A\right)\left(y_M-y_A\right)\right|\)
\(=\dfrac{1}{2}\left|4\left(m^2-1\right)-8\left(m+1\right)\right|=2\left|m^2-2m-3\right|\)
Do \(m^2-2m-3< 0;\forall m\in\left(-1;3\right)\)
\(\Rightarrow S=-2\left(m^2-2m-3\right)=8-2\left(m-1\right)^2\le8\)
Dấu "=" xảy ra khi \(m=1\) hay \(M\left(1;1\right)\)