Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐÁP ÁN C
Gọi vectơ pháp tuyến của đường thẳng cần tìm là n Δ → ( a ; b ) ( a 2 + b 2 > 0 )
Đường thẳng d có VTPT là n d → ( 1 ; − 1 )
Để đường thẳng d tạo với đường thẳng ∆ góc 450 nên ta có:
cos 45 0 = c os ( n d → ; n Δ → ) = 1. a − 1. b 1 2 + ( − 1 ) 2 . a 2 + b 2 ⇔ 1 2 = a − b 2 . a 2 + b 2 ⇔ a 2 + b 2 = a − b ⇔ a 2 + b 2 = a 2 − 2 a b + b 2 ⇔ 2 a b = 0 ⇔ a = 0 b = 0
* Nếu a = 0 thì chọn b = 1 . Đường thẳng ∆ nhận vecto (0; 1) làm VTPT và qua A( 1;3) nên có
phương trình là 0 (x- 1) + 1( y – 3) = 0 hay y – 3 = 0.
* Nếu b = 0 thì chọn a =1. Đường thẳng ∆ nhận vecto (1; 0) làm VTPT và qua A(1;3) nên có
phương trình là 1 (x- 1) + 0( y – 3) = 0 hay x= 1
Vậy có 2 đường thẳng thỏa mãn là: y – 3 =0 và x = 1

ĐÁP ÁN B
Đường thẳng qua A và tạo với d1d2 các góc bằng nhau khi vuông góc với phân giác của góc tạo bởi d1d2.
Do vậy số lượng đường thẳng cần tìm là 2.

Gọi \(\left(a;b\right)\) là 1 vtpt của d
\(\overrightarrow{AC}=\left(5;-2\right)\Rightarrow\) đường thẳng AC nhận (2;5) là 1 vtpt
Do góc giữa d và AC bằng 45 độ
\(\Rightarrow cos45^0=\dfrac{1}{\sqrt{2}}=\dfrac{\left|2a+5b\right|}{\sqrt{2^2+5^2}.\sqrt{a^2+b^2}}\)
\(\Leftrightarrow29\left(a^2+b^2\right)=2\left(2a+5b\right)^2\)
\(\Leftrightarrow21a^2-40ab-21b^2=0\)
\(\Leftrightarrow\left(3a-7b\right)\left(7a+3b\right)=0\)
Chọn \(\left(a;b\right)=\left[{}\begin{matrix}\left(7;3\right)\\\left(3;-7\right)\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}7\left(x-3\right)+3\left(y-5\right)=0\\3\left(x-3\right)-7\left(y-5\right)=0\end{matrix}\right.\)

Lời giải:
VTPT của $(d)$: $(2,-3)$
Đường thẳng $\Delta$ vuông góc với $(d)$ nên VTCP của $(\Delta)$ chính là $(2,-3)$
$\Rightarrow$ VTPT $ của $(\Delta)$ là $(3,2)$
PTĐT $(\Delta)$: $3(x-1)+2(y-2)=0$
$\Leftrightarrow 3x+2y-7=0$

Đáp án B
Gọi ∆ là đường thẳng cần tìm và
![]()
Để ∆ tạo với đường thẳng ( d) một góc 450 thì:

Tương đương : 2( A+ 3B) 2= 10( A2+ B2)
Nên A= 2B hoặc B= -2A
+ Với A= 2B, chọn B= 1 thì A= 2 ta được phương trình ∆ : 2x + y + 4= 0.; có hệ số góc là k= -2
+ Với B= -2A, chọn A= 1 thì B= -2 ta được phương trình ∆: x- 2y+ 2 = 0 ; có hệ số góc là k= 1/2
Vậy tổng các hệ số góc là:
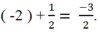

d nhận \(\left(2;3\right)\) là 1 vtpt nên nhận \(\overrightarrow{u}=\left(3;-2\right)\) là 1 vtcp
Do \(B\in d\) nên tọa độ có dạng: \(B\left(b;\dfrac{-2b-4}{3}\right)\Rightarrow\overrightarrow{AB}=\left(b-1;\dfrac{-2b-7}{3}\right)\)
\(cos45^0=\dfrac{\left|3.\left(b-1\right)+\dfrac{2\left(2b+7\right)}{3}\right|}{\sqrt{3^2+2^2}.\sqrt{\left(b-1\right)^2+\left(\dfrac{2b+7}{3}\right)^2}}=\dfrac{1}{\sqrt{2}}\)
\(\Leftrightarrow2\left(13b+5\right)^2=13\left(13b^2+10b+58\right)\)
\(\Leftrightarrow169b^2+130b-704=0\Rightarrow\left[{}\begin{matrix}b=-\dfrac{32}{13}\\b=\dfrac{22}{13}\Rightarrow y_B=-\dfrac{32}{13}< 0\left(loại\right)\end{matrix}\right.\)
Đường thẳng d có VTPT n d → ( 2 ; − 3 )
Gọi đường thẳng ∆ thỏa mãn có VTPT n Δ → ( a ; b )
Vì góc giữa hai đường thẳng bằng 600 nên:
cos 60 0 = c os ( n d → ; n Δ → ) = 2 a − 3 b 2 2 + ( − 3 ) 2 . a 2 + b 2 ⇔ 1 2 = 2 a − 3 b 13 . a 2 + b 2 ⇔ 13 . a 2 + b 2 = 2. 2 a − 3 b ⇔ 13 ( a 2 + b 2 ) = 4 ( 4 a 2 − 12 a b + 9 b 2 ) ⇔ − 3 a 2 + 48 a b − 23 b 2 = 0 ⇔ − 3 a b 2 + 48. a b − 23 = 0 ( * )
Phương trình (*) có 2 nghiệm phân biệt. Ứng với mỗi nghiệm ta tìm được 1 cặp số (a, b) là VTPT của đường thẳng ∆. Từ đó, ta viết được 2 phương trình đường thẳng ∆ thỏa mãn.
ĐÁP ÁN C