Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(α) vuông góc với giá của a → ⇒ (α) nhận a → là 1 vtpt.
(α) đi qua A(-1; 2; -3)
⇒ (α): 6x – 2y – 3z + 1 = 0.

Chọn D
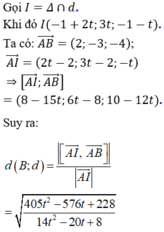
Xét hàm số:
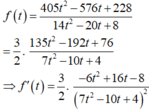
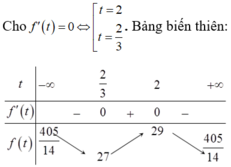
Do đó d (B; d) nhỏ nhất khi f(t) đạt giá trị nhỏ nhất bằng 27 tại t = 2/3. Suy ra ![]() . Chọn một vectơ chỉ phương của đường thẳng d là
. Chọn một vectơ chỉ phương của đường thẳng d là ![]()
Vậy phương trình đường thẳng ![]()

Chọn C
Gọi d là đường thẳng cần tìm.

Đường thẳng cần tìm qua A và nhận ![]() là véc tơ chỉ phương nên có phương trình:
là véc tơ chỉ phương nên có phương trình:
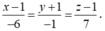

Ta có: a d → = (2; −1; 4)
Xét điểm B(–3 + 2t; 1 – t; –1 + 4t) thì AB → = (1 + 2t; 3 − t; −5 + 4t)
AB ⊥ d ⇔ AB → . a d → = 0
⇔ 2(1 + 2t) − (3 − t) + 4(−5 + 4t) = 0 ⇔ t = 1
Suy ra AB → = (3; 2; −1)
Vậy phương trình của
∆
là 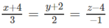

Do \(\Delta\) đi qua A và vuông góc với d nên \(\Delta\) phải nằm trong mặt phẳng (P) đi qua A và vuông góc với d.
Mặt phẳng (P) nhận vecto \(\overrightarrow{u}=\left(2;-1;4\right)\) của d làm vecto pháp tuyến, đi qua A(-4;-2;4) có phương trình : \(2x-y+4z-10=0\)
Gọi M là giao điểm của d và (P) thì M(-3+2t;1-t;-1+4t) thuộc d và M thuộc \(\Delta\)
Ta cũng có : \(M\in\left(P\right)\Leftrightarrow2\left(-3+2t\right)-\left(1-t\right)+4\left(-1+4t\right)-10=0\) \(\Leftrightarrow21t-21=0\Leftrightarrow t=1\)Vậy \(M\left(-1;0;3\right)\)Khi đó \(\overrightarrow{MA}=\left(3;2;-1\right)\), đường thẳng \(\Delta\)đi qua A và M có phương trình :\(\frac{x+4}{3}=\frac{y+2}{2}=\frac{z-4}{-1}\)
a. (P) vuông góc denta nên nhận (1;2;3) là 1 vtpt
Phương trình (P):
\(1\left(x-2\right)+2\left(y-1\right)+3\left(z-3\right)=0\)
\(\Leftrightarrow x+2y+3z-13=0\)
b. \(\overrightarrow{AB}=\left(1;2;-1\right)\) ; \(\overrightarrow{n_{\left(P\right)}}=\left(1;1;1\right)\)
\(\left[\overrightarrow{AB};\overrightarrow{n_{\left(P\right)}}\right]=\left(3;-2;-1\right)\)
Phương trình mp:
\(3\left(x-1\right)-2\left(y+1\right)-1\left(z-2\right)=0\)
\(\Leftrightarrow3x-2y-z-3=0\)




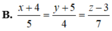
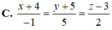
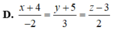

(α) ⊥ a →
Δ ⊥ a →
⇒ Δ song song hoặc nằm trong (α).
Mà Δ và (α) cùng đi qua A
⇒ Δ ⊂ (α)
Δ cắt d ⇒ Δ cắt d tại M
⇒ Δ chính là đường thẳng AM.