Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Sửa đề: $z$ đầu tiên ở mẫu đổi thành $a$.
Ta có:
$\frac{bz-cy}{a}=\frac{cx-az}{b}=\frac{ay-bx}{c}$
$=\frac{abz-cya}{a^2}=\frac{bcx-abz}{b^2}=\frac{acy-bcx}{c^2}$
$=\frac{abz-cya+bcx-abz+acy-bcx}{a^2+b^2+c^2}=\frac{0}{a^2+b^2+c^2}=0$
$\Rightarrow bz-cy=cx-az=ay-bx=0$
$\Rightarrow bz=cy; cx=az; ay=bx$
$\Rightarrow \frac{x}{a}=\frac{y}{b}=\frac{z}{c}$
Ta có đpcm.

Ta có :
\(\dfrac{cy-bz}{x}=\dfrac{az-cx}{y}=\dfrac{bx-ay}{z}=\dfrac{bxz-cxy+cxy-ayz+ayz-bxz}{ax+by+cz}=0\)
\(\Rightarrow\dfrac{cy-bz}{x}=0\Rightarrow cy=bz\Rightarrow\dfrac{b}{y}=\dfrac{c}{z}\left(1\right)\)
\(\Rightarrow\dfrac{az-cx}{y}=0\Rightarrow az=cx\Rightarrow\dfrac{a}{x}=\dfrac{c}{z}\left(2\right)\)
Từ (1) và (2) suy ra:\(\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}\)

Ta có :
\(\dfrac{cy-bx}{x}=\dfrac{az-cx}{y}=\dfrac{bx-ay}{z}=\dfrac{bxz-cxy+cxy-ayz+ayz-bxz}{ax+by+cz}=0\)
\(\Rightarrow\dfrac{cy-bz}{x}=0\) \(\Rightarrow cy=bz\) \(\Rightarrow\) \(\dfrac{b}{y}=\dfrac{c}{z}\left(1\right)\)
\(\Rightarrow\dfrac{az-cx}{y}=0\) \(\Rightarrow az=cx\) \(\Rightarrow\dfrac{a}{x}=\dfrac{c}{z}\left(2\right)\)
Từ (1) và (2) suy ra : \(\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}\)

10 người cùng cày trên 1 cánh đồng hết 10,5 h
a)Hỏi nếu 5 máy cùng cày trên 9 mảnh ruộng như thế hết bao nhiêu thời gian ,biết rằng năng xuất của 1 máy =15 người và cày 1 cánh đồng 3h
b)cho chu vi mảnh ruộng là 18 m , và chiều dài tỉ lệ với chiều rộng là 5:1 . hỏi giá tiền của phải trả cho người cày hết 9 mảnh ruộng đó là bao nhiêu tiền biết 1m2 phải trả 10000 đồng

Đặt \(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=k\) thì \(x=ak,y=bk,z=ck\)
\(\dfrac{bz-cy}{a}=\dfrac{bck-bck}{a}=0\) __( 1 )__
\(\dfrac{cx-az}{b}=\dfrac{ack-ack}{b}=0\) __( 2 )__
\(\dfrac{ay-bx}{c}=\dfrac{abk-abk}{c}=0\) __( 3 )__
Từ ( 1 ), ( 2 ), ( 3 ) suy ra \(\dfrac{bz-cy}{a}=\dfrac{cx-az}{b}=\dfrac{ay-bx}{c}\)
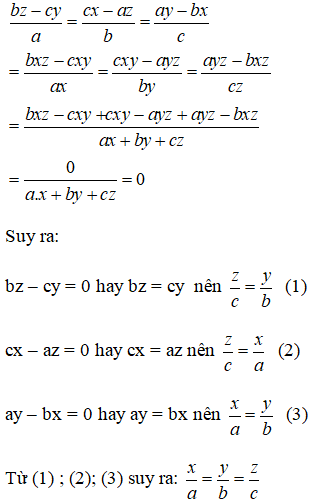
Click vào đây để nhận được câu trả lời