Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

C E M M A B
a) Vì tam giác DEM cân tại D =) DA=DM
Vì EB; MA lần lượt là các đường trung tuyến của tam giác DEM, cắt nhau tại C nên C là trọng tâm
Suy ra DC cũng là đg trung tuyến của tam giác DM.
Tam giác DEM cân có DC là trung tuyến(cmt) nên DC cũng là đg phân giác=) ^EDC=^MDC
CMĐC: Tam giác DCM= Tam giác DCE
b) Tam giác ABC có: AC+ CB>AB(1)
Vì tam giác DEM có MA; EB lần lượt là các đg t.t=) A;B lần lượt là trung điểm DE; DM
Suy ra AB=1/2EM và AB//EM (Tính chất đường trung bình)(2)
CMđược: tam giác ADC= tam giác BDC(c-g-c)
=)CA=CB(3)
Từ (1) và (3)=)2AC>AB=)4AB>2AB(4)
Từ (2) và (4)=) EM<4AC

Bài 1:
a: Xét ΔBAD vuong tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
Do đó: ΔBAD=ΔBED
SUy ra: DA=DE
b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
góc ADF=góc EDC
Do đó:ΔADF=ΔEDC
Suy ra: DF=DC
hay ΔDFC cân tại D

Chỉ vô tình vào chém thôi
CM: BE vuông góc DC. dễ chứng minh bằng cặp tam giác bằng nhau
Có MH là đg tb tam giác BCE thì MH//BE và MH=1/2BE
MK là đg trung bình tam giác BDC thì MK//DC và MK=1/2CD
Do đó MK=MH do BE=DC
Và MK vuông góc MH

BÀI 1 cho tam giác ABC vuông tại A.Kẻ BD là phân giác của góc B.Kẻ AI vuông góc BD tại I.AI cắt BC tại E
a) chứng minh AB=EB
b) chứng minh tam giác BED vuông
c) DE cắt AB tại F, chứng minh AE//FC
BÀI 2 cho tam giác ABC cân tại A, có BD và CE là hai đường trung tuyến cắt nhau tại I
a) chứng minh tam giác IBC cân
b)lấy O thuộc tia IC sao cho IO=IE.Gọi K là trung điểm của IA.Chứng minh AO, BD, CK đồng quy
BÀI 3 cho tam giác ABC cân tại A, kẻ tia phân giác của góc BAC cắt BC tại H.Biết AB=15cm, BC=18cm
a)so sánh góc A và góc C
b)chứng minh rằng tam giác ABH = tam giác ACH
c)vẽ trung tuyến BD của tam giác ABC cắt AH tại G.Chứng minh rằng: tam giác AEG = tam giác ADG
d)tính độ dài AG
e) kẻ đường thẳng CG cắt AB ở E, chứng minh rằng: tam giác AEG = tam giác ADG
BÀI 4 cho tam giác ABC vuông tại A, trên BC lấy điểm D sao cho BA=BD.Qua D kẻ đường vuông góc với BC cắt AC tại E, qua C kẻ đường vuông góc với BE tại H cắt AB tại F
a)chứng minh tam giác ABE = tam giác DBE
b) chứng minh tam giác BCF cân
c) chứng minh 3 điểm F.D,E thẳng hàng
d)trên cạnh CB lấy điểm M sao cho CA=CM.Tính số đo góc DAM
BÀI 5 cho tam giác ABC cân tại A, kẻ BD vuông góc AC, kẻ CE vuông góc AB, BD và CE cắt nhau tại I
a)chứng minh rằng tam giác BDC = tam giác CEB
b)so sánh góc IBE và góc ICD
c) đường thẳng AI cắt BC tại H, chứng minh AI vuông góc BC tại H
BÀI 6 cho tam giác ABC vuông tại A, biết AB=6cm, AC=8cm
a)tính BC
b)trung trực của BC cắt AC tại D và cắt AB tại F, chứng minh góc DBC=DCB
c) trên tia đối của tia DB lấy E sao cho DE=DC, chứng minh tam giác BCE vuông và DF là phân giác góc ADE
d) chứng minh BE vuông góc FC
Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).

a) Xét 2 tam giác vuông BCK & CBH có:
B = C
BC chung
=>tam giác BCK = CBH ( cạnh huyền - góc nhọn)
b) Ta có : IBC = ICB ( 2 góc tương ứng)
=> tam giác IBC là tam giác cân

Lời giải:
Bài 1:
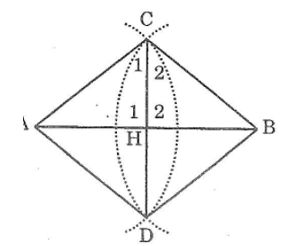
Gọi H là giao điểm của AB và CD
Nối AC, AD,BC,BD
Xét ΔACD và ΔBCD, ta có:
AC = BC
(bán kính hai cung tròn bằng nhau)
AD = BD
CD cạnh chung
Suy ra: ΔACD= ΔBCD(c.c.c)
Suy ra: ∠C2 =∠C2 (hai góc tương ứng)
Xét hai tam giác AHC và BHC. Ta có:
AC = BC (bán kính hai cung tròn bằng nhau)
∠C2 =∠C2 (chứng minh trên)
CH cạnh chung
Suy ra: ΔAHC= ΔBHC(c.g.c)
Suy ra: AH = BH (hai cạnh tương ứng) (1)
Ta có : ∠H1 =∠H2 (hai góc tương ứng)
∠H1 + ∠H2 =180° (hai góc kề bù)
Suy ra: ∠H1 =∠H2 =90° => CD ⊥ AB (2)
Từ (1) và (2) suy ra CD là đường trung trực của AB
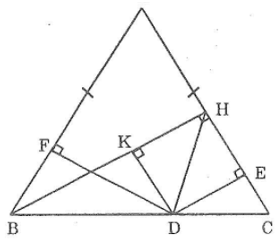
bài 2
Kẻ DK ⊥ BH
Ta có: BH ⊥AC(gt)
Suy ra: DK // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song)
=> ∠KDB =C (hai góc đồng vị)
VìΔABC cân tại A nên ∠B =∠C (tính chất tam giác cân)
Suy ra: ∠KDB =B
Xét hai tam giác vuông BFD và DKB, ta có:
∠BFD =∠DKB
BD cạnh huyền chung
∠FBD =∠KDB (chứng minh trên)
Suy ra:ΔBFD=ΔDKB(cạnh huyền góc nhọn)
=> DF = BK (hai cạnh tương ứng)(1)
Nối DH. XétΔDEHvàΔDKH, ta có:
∠DEH =∠DKH =90°
DH cạnh huyền chung
∠EHD =∠KDH (hai góc so le trong)
Suy ra:ΔDEH=ΔDKH( cạnh huyền , góc nhọn)
Suy ra: DE = HK ( hai cạnh tương ứng) (2)
Mặt khác : BH = BK + KH (3)
Từ (1), (2) và (3) suy ra: DF = DE = BH
cho tớ hỏi đề bài sai à
làm gì có điểm H