Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha
Bài giải
a, Ta có : Tổng 3 trong một tam giác bằng 1800
=> \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
Hay : \(\widehat{A}=180^0-\left(\widehat{B}+\widehat{C}\right)\)
\(\Rightarrow\widehat{A}=180^0-\left(70^0+30^0\right)\)
\(\Rightarrow\widehat{A}=80^0\)
Mặt khác : tia phân giác của góc A cắt ABC tại D
\(\Rightarrow\widehat{BAD}=\widehat{DAC}=\frac{80^0}{2}=40^0\)
Ta có : \(\widehat{ADC}=180^0-\left(\widehat{DAC}+\widehat{C}\right)\)
\(\Rightarrow\widehat{ADC}=180^0-\left(40^0+30^0\right)\)
\(\Rightarrow\widehat{ADC}=110^0\)

a: \(\widehat{BAC}=180^0-70^0-30^0=80^0\)
=>\(\widehat{CAD}=40^0\)
\(\widehat{ADC}=180^0-40^0-30^0=110^0\)
b: \(\widehat{B}-\widehat{C}=40^0\)
nên \(\widehat{B}=\widehat{C}+40^0\)
Ta có: \(\widehat{ABD}+\widehat{ADB}+\widehat{BAD}=\widehat{ACD}+\widehat{ADC}+\widehat{CAD}\)
\(\Leftrightarrow\widehat{C}+40^0+\widehat{ADB}=\widehat{C}+\widehat{ADC}\)
\(\Leftrightarrow\widehat{ADB}-\widehat{ADC}=-40^0\)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)
nên \(-2\cdot\widehat{ADC}=\dfrac{-40^0-180^0}{2}=-110^0\)
hay \(\widehat{ADC}=55^0\)

a) ∆ADB và ∆ ACD có:
\(\widehat{B}\) =\(\widehat{C}\)(gt) (1)
\(\widehat{A1}\)=\(\widehat{A2}\)(AD là tia phân giác)
Nên \(\widehat{D1}\)=\(\widehat{D2}\)
AD cạnh chung.
Do đó ∆ADB=∆ADC(g.c.g)
b) ∆ADB=∆ADC(câu a)
Suy ra AB=AC .
a Xét \(\Delta ADB\) và \(\Delta ADC\) có :
AD : cạnh chung
\(\widehat{BAD}=\widehat{CAD}\) (gt)
Ta có : \(\widehat{BDA}+\widehat{DAB}+\widehat{ABD}=\widehat{CDA}+\widehat{DAC}+\widehat{ACD}\)
\(\Rightarrow\widehat{BDA}=\widehat{CDA}\)
\(\Rightarrow\Delta ADB=\Delta ADC\) (g . c . g)
b Vì \(\Delta ADB=\Delta ADC\)
\(\Rightarrow\) AB = AC
![]()

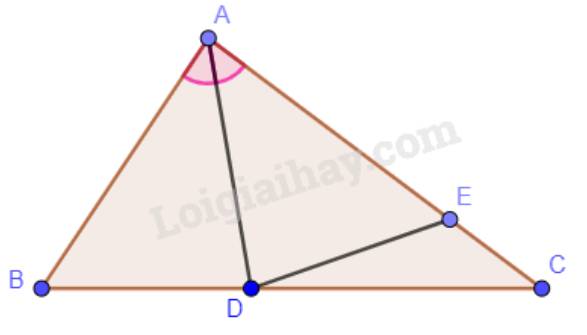
a) Ta có: \(\widehat {BAD} = \widehat {CAD}\)(vì AD là phân giác của góc BAC).
Mà \(\widehat B > \widehat C\)nên \(\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\\ \to 180^\circ - (\widehat B + \widehat {BAD}) < 180^\circ - (\widehat C + \widehat {CAD})\\ \to \widehat {ADB} < \widehat {ADC}\end{array}\)
b) Xét hai tam giác ADB và tam giác ADE có:
\(\widehat {ADB} = \widehat {ADE}\);
AD chung;
\(\widehat {BAD} = \widehat {EAD}\).
Vậy \(\Delta ABD = \Delta AED\) (g.c.g)
Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.
Trong tam giác ABC có \(\widehat B > \widehat C\) nên AC > AB hay AB < AC (AB là cạnh đối diện với góc C, AC là cạnh đối diện với góc B).

Answer:
A) Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{A}=180^o-\widehat{B}-\widehat{C}\)
\(\Rightarrow\widehat{A}=180^o-100^o=80^o\)
\(\Rightarrow\widehat{DAC}=\frac{\widehat{A}}{2}=40^o\)
B) Ta có: \(\widehat{ADC}=\widehat{B}+\frac{1}{2}\widehat{A}\)
\(=\widehat{A}+\widehat{B}+\widehat{B}\)
\(=180^o-\widehat{C}+\widehat{B}\)
\(=180^o-\left(\widehat{B}-\widehat{C}\right)=140^o\)
Ta có
góc ADC=góc DAB+ góc B (theo tính chất góc ngoài của tam giác)
góc ADB= góc DAC + góc C
=> góc ADC- góc ADB=góc B+ góc DAB-(góc C+ góc DAC)
Vì AD là tia phân giác của góc A
=> góc DAB= góc DAC
=>góc ADC- góc ADB=gocsB-góc C=40 độ
mà góc ADC và góc ADB là 2 góc kề bù
=> góc ADC+góc ADB=180 độ
=> góc ADC=(180 độ +40 độ):2=110 độ
KL