Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét 2 \(\Delta\) \(ABI\) và \(DBI\) có:
\(AB=DB\left(gt\right)\)
\(\widehat{ABI}=\widehat{DBI}\) (vì \(BI\) là tia phân giác của \(\widehat{B}\))
Cạnh BI chung
=> \(\Delta ABI=\Delta DBI\left(c-g-c\right)\)
=> \(IA=ID\) (2 cạnh tương ứng).
b) Xem lại đề.
c) Theo câu a) ta có \(\Delta ABI=\Delta DBI.\)
=> \(\widehat{BAI}=\widehat{BDI}\) (2 góc tương ứng).
Mà \(\widehat{BAI}=90^0\left(gt\right)\)
=> \(\widehat{BAI}=\widehat{BDI}=90^0.\)
Xét 2 \(\Delta\) vuông \(IAE\) và \(IDC\) có:
\(\widehat{EAI}=\widehat{CDI}=90^0\)
\(IA=ID\left(cmt\right)\)
\(\widehat{AIE}=\widehat{DIC}\) (vì 2 góc đối đỉnh)
=> \(\Delta IAE=\Delta IDC\) (cạnh góc vuông - góc nhọn kề).
b) Vì \(BI\) là tia phân giác của \(\widehat{B}\left(gt\right)\)
=> \(BH\) là tia phân giác của \(\widehat{B}.\)
Theo câu c) ta có \(\Delta IAE=\Delta IDC.\)
=> \(AE=DC\) (2 cạnh tương ứng).
Ta có:
\(\left\{{}\begin{matrix}BA+AE=BE\\BD+DC=BC\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}BA=BD\left(gt\right)\\AE=DC\left(cmt\right)\end{matrix}\right.\)
=> \(BE=BC.\)
=> \(\Delta EBC\) cân tại B.
Có \(BH\) là đường phân giác (cmt).
=> \(BH\) đồng thời là đường cao của \(\Delta EBC.\)
=> \(BH\perp CE\left(đpcm\right).\)
Chúc bạn học tốt!

Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau

a: Xét ΔABI và ΔDCI có
IA=ID
\(\widehat{AIB}=\widehat{DIC}\)
IB=IC
Do đó: ΔABI=ΔDCI
Suy ra: \(\widehat{ABI}=\widehat{DCI}\)
mà hai góc này ở vị trí so le trong
nên AB//CD
b: Ta có: AB//CD
mà AB\(\perp\)AC
nên CD\(\perp\)AC
c: Xét tứ giác ABDC có
I là trung điểm của AD
I là trung điểm của BC
Do đó: ABDC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: BC=AD

a: Xét ΔBAH vuông tại A và ΔBEH vuông tại E có
BH chung
góc ABH=góc EBH
=>ΔBAH=ΔBEH
=>BA=BE
=>ΔBAE cân tại B
b: Xét ΔBFC có
FE,CA là đường cao
FE cắt CA tại H
=>H là trực tâm
=>HK vuông góc FC
c: Xét tứ giác QAKF có
M là trung điểm chung của QK và AF
=>QAKF là hình bình hành
=>QA//FK
=>Q,E,A thẳng hàng

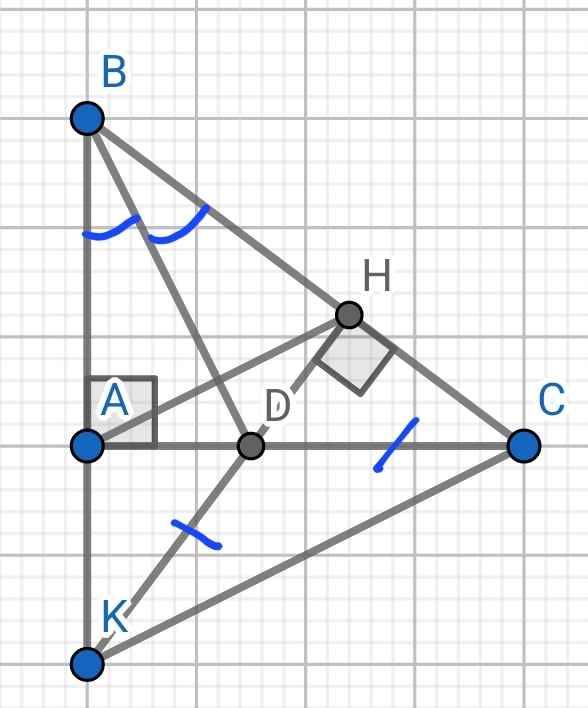
a) Xét hai tam giác vuông: ∆ABD và ∆HBD có:
BD chung
∠ABD = ∠HBD (BD là phân giác của ∠ABH)
⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)
b) Do ∆ABD = ∆HBD (cmt)
⇒ AB = BH (hai cạnh tương ứng)
⇒ B nằm trên đường trung trực của AH (1)
Do ∆ABD = ∆HBD (cmt)
⇒ AD = HD (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AH (2)
Từ (1) và (2) ⇒ BD là đường trung trực của AH
c) Xét ∆ADK và ∆HDC có:
AD = HD (cmt)
∠ADK = ∠HDC (đối đỉnh)
DK = DC (gt)
⇒ ∆ADK = ∆HDC (c-g-c)
⇒ ∠DAK = ∠DHC (hai góc tương ứng)
⇒ ∠DAK = 90⁰
Mà ∠DAB = 90⁰
⇒ ∠DAK + ∠DAB = 180⁰
⇒ B, A, K thẳng hàng

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔAHB=ΔAKC