Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

→IB+→IA−→IC−→CM=→0
=>\(\overrightarrow{IB}+\overrightarrow{IA}-\overrightarrow{IM}=\overrightarrow{0}\)
=>\(\overrightarrow{IB}+\overrightarrow{IA}=\overrightarrow{IM}\)
Đặt K là trung điểm AB
=>\(\overrightarrow{IB}+\overrightarrow{IA}=\overrightarrow{2IK}\)(T/c trung tuyến)
=>\(\overrightarrow{2IK}=\overrightarrow{IM}\)
=>K,M,I thẳng hàng
Vậy điểm M thuộc đoạn KI sao cho \(\dfrac{\overrightarrow{IK}}{\overrightarrow{IM}}=\dfrac{1}{2}\)

\(\overrightarrow{AM}-\overrightarrow{AN}=\overrightarrow{NM}\)
\(\overrightarrow{MN}-\overrightarrow{NC}=\overrightarrow{CM}\)

Câu 2:
Vì G là trọng tâm nên \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
hay \(\overrightarrow{GC}=-\overrightarrow{a}-\overrightarrow{b}\)
\(\overrightarrow{BC}=\overrightarrow{BG}+\overrightarrow{GC}=-\overrightarrow{b}-\overrightarrow{a}-\overrightarrow{b}=-\overrightarrow{a}-2\overrightarrow{b}\)
=>m=-1; n=-2

Do G là trọng tâm ABC \(\Rightarrow\overrightarrow{BG}=\dfrac{1}{3}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}\)
I đối xứng B qua G \(\Rightarrow\) \(\overrightarrow{BI}=2\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BC}=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(\Rightarrow\overrightarrow{BI}=\dfrac{4}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{AC}=-\dfrac{4}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{CI}=\overrightarrow{CB}+\overrightarrow{BI}=\overrightarrow{CA}+\overrightarrow{AB}-\dfrac{4}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{CI}=-\dfrac{1}{3}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}\)

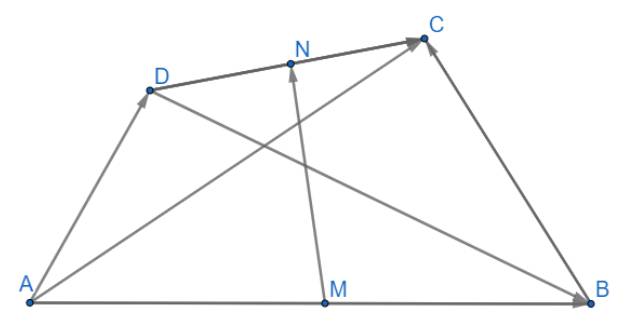
a) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {ND} \\= \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) \\= \overrightarrow 0 + 2\overrightarrow {MN} + \overrightarrow 0 = 2\overrightarrow {MN} \) (đpcm)
b) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
\(\)\(\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND} \)
\(\left( {\overrightarrow {BM} + \overrightarrow {AM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) = 2\overrightarrow {MN} \)
Mặt khác ta có: \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN} \)
Suy ra \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
Cách 2:
\(\begin{array}{l}
\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \\
\Leftrightarrow \overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {BC} - \overrightarrow {BD} \\
\Leftrightarrow \overrightarrow {DC} = \overrightarrow {DC} (đpcm)
\end{array}\)
a)\(\overrightarrow{AB}+\overrightarrow{AN}=\overrightarrow{AM}\)
b)\(\overrightarrow{BA}+\overrightarrow{CN}=2\overrightarrow{BA}\)
c)Có \(\overrightarrow{AB}=\overrightarrow{NC}\)=>bt trở thành \(\overrightarrow{NC}+MC+\overrightarrow{MN}=\overrightarrow{MC}-\overrightarrow{MC}=vt0\)
d)có vt BA+vt BC=vtBN
bt trở thành vtMN-vtMN=vt0
hok tốt!