Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

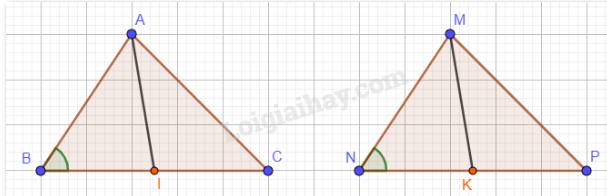
Hai tam giác ABC và MNP có: AB = MN, BC = NP, CA = PM nên \(\Delta ABC = \Delta MNP\)(c.c.c)
Suy ra: \(\widehat {ABI} = \widehat {MNK}\) ( 2 góc tương ứng).
Ta có: I, K lần lượt là trung điểm của BC và NP mà BC = NP, suy ra: \(BI = NK\).
Xét tam giác ABI và tam giác MNK có:
AB = MN;
\(\widehat {ABI} = \widehat {MNK}\);
BI = NK.
Vậy \(\Delta ABI = \Delta MNK\)(c.g.c). Suy ra: AI = MK (2 cạnh tương ứng).
Vậy AI = MK.


Ta có: \(\Delta ABC = \Delta MNP\) nên theo tính chất 2 tam giác bằng nhau, ta có:
\(\begin{array}{l}\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\\AB = MN,BC = NP,AC = NP.\end{array}\)
Mà AD và MQ lần lượt là phân giác của góc BAC và NMP nên \(\widehat {BAD} = \widehat {NMQ} = \dfrac{1}{2}\widehat {BAC} = \dfrac{1}{2}\widehat {NMP}\).
Xét hai tam giác ABD và MNQ có:
\(\widehat {BAD} = \widehat {NMQ}\);
AB = MN;
\(\widehat B = \widehat N\).
Vậy \(\Delta ABD = \Delta MNQ\) (g.c.g) nên AD = MQ ( 2 cạnh tương ứng)

a) Xét \(\Delta DNA\) và \(\Delta BCN\), có:
DN = NB (gt)
góc N1 = N2 (2 góc đối đỉnh)
AN = CN (N là TĐ của AC)
->\(\Delta DNA=\Delta BCN\) (c.g.c)
-> AD = BC (2 cạnh tương ứng)
-> góc A1 = góc ACB ( 2 góc tương ứng)
Mà góc A1 và góc ACB là 2 góc SLT
-> AD//BC
Mình chỉ làm được ý a thôi hihi thông cảm

xét tam giác AMB và tam giác CMD có
AM = MC (gt)
góc AMB = góc CMD ( đối đỉnh )
BM = MD (gt)
do đó tam giác AMB = tam giác CMD (c.g.c)

a) Xét hai tam giác ABD và tam giác MNQ:
AB = MQ (do \(\Delta ABC = \Delta MNP\)).
\(\widehat {ABD} = \widehat {MNQ}\) (\(\widehat {ABD} = \widehat {MNQ}\)).
BD = NQ (\(\dfrac{1}{2}BC = \dfrac{1}{2}NP\))
BC = NP (do \(\Delta ABC = \Delta MNP\)).
Vậy \(\Delta ABD = \Delta MNQ\)(c.g.c) nên AD = MQ ( 2 cạnh tương ứng)
b) Vì \(\Delta ABC = \Delta MNP\) nên BC = NP ( 2 cạnh tương ứng) . Do đó, \(\dfrac{1}{2}BC = \dfrac{1}{2}NP\) hay DC = QP
Vì \(\Delta ABC = \Delta MNP\) nên AC = MP ( 2 cạnh tương ứng) . Do đó, \(\dfrac{1}{2}AC = \dfrac{1}{2}MP\) hay EC = RP
Xét hai tam giác DEC và tam giác QRP:
DC = QP
\(\widehat {ECD} = \widehat {RPQ}\)(\(\Delta ABC = \Delta MNP\))
EC = RP
Vậy \(\Delta DEC = \Delta QRP\)(c.g.c) nên DE = QR ( 2 cạnh tương ứng)