Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vẽ đường thẳng song song với AC và vuông góc với AB tài D và N ( góc NDA = 90 độ)
Xét tam giác NAD và tam giác NAH có :
góc DAN = góc NAH ( vì DN là tia p/g góc BAH)
AN cạnh chung
=> tam giác NAD = tam giác NAH ( ch-gn)
=> góc DNA = góc ANH ( hai góc tương ứng ) (1)
Mặt khác : góc DNA = góc NAC ( hai góc so le trong )
Kết hợp (1) => góc DNA = góc ANH = góc NAC => tam giác NCA cân tại C => NC =AC (3)
Xét tam giác NCI và tam giác ACI có:
NC =AC ( do (3))
CI cạnh chung
góc NCI = góc ICA ( CI là p/g góc BCA)
=> tam giác NCI = tam giác ACI ( c.g.c)
=> góc NIC = góc AIC ( hai góc tương ứng )
Mà góc NIC và góc AIC là cặp góc kề bù
=> góc NIC = góc AIC = 90 độ
**** bạn

Vẽ đường thẳng song song với AC và vuông góc với AB tài D và N ﴾ góc NDA = 90 độ﴿
Xét tam giác NAD và tam giác NAH có :
góc DAN = góc NAH ﴾ vì DN là tia p/g góc BAH﴿
AN cạnh chung
=> tam giác NAD = tam giác NAH ﴾ ch‐gn﴿
=> góc DNA = góc ANH ﴾ hai góc tương ứng ﴿ ﴾1﴿
Mặt khác : góc DNA = góc NAC ﴾ hai góc so le trong ﴿
Kết hợp ﴾1﴿ => góc DNA = góc ANH = góc NAC => tam giác NCA cân tại C => NC =AC ﴾3﴿
Xét tam giác NCI và tam giác ACI có: NC =AC ﴾ do ﴾3﴿﴿
CI cạnh chung
góc NCI = góc ICA ﴾ CI là p/g góc BCA﴿
=> tam giác NCI = tam giác ACI ﴾ c.g.c﴿
=> góc NIC = góc AIC ﴾ hai góc tương ứng ﴿
Mà góc NIC và góc AIC là cặp góc kề bù
=> góc NIC = góc AIC = 90 độ(đpcm)

Vẽ đường thẳng song song với AC và vuông góc với AB tại D và N \(\left(\widehat{NDA}=90^0\right)\)
Xét t.giác NAD và t.giác NAH có :
\(\widehat{DAN}=\widehat{NAH}\)( vì DN là tia phân giác của góc BAH )
AN : cạnh chung
=> T.giác NAD = t.giác NAH ( ch-gn )
\(\Rightarrow\widehat{DNA}=\widehat{ANH}\)( 2 góc tương ứng ) (1)
Mặt khác : \(\widehat{DNA}=\widehat{NAC}\)( hai góc so le trong )
Từ (1) => \(\widehat{DNA}=\widehat{ANH}=\widehat{NAC}\)=> T.giác NCA cân tại C => NC = AC (2)
Xét t.giác NCI và t.giác ACI có :
NC = AC ( do (3))
\(\widehat{NCI}=\widehat{ICA}\)( CI là tia phâ giác góc BCA )
CI : cạnh chung
=> T.giác NCI = T.giác ACI ( c-g-c )
\(\Rightarrow\widehat{NIC}=\widehat{AIC}\)( hai góc tương ứng )
Mà góc NIC và góc AIC là cặp góc kề bù
\(\Rightarrow\widehat{NIC}=\widehat{AIC}=90^0\left(đpcm\right)\)

Ta có hình vẽ:
Vì AI là phân giác của BAH nên \(BAI=HAI=\frac{BAH}{2}\)
CI là phân giác của BCA nên \(BCI=ACI=\frac{BCA}{2}\)
Δ ABC vuông tại A có: ABC + BCA = 90o
=> BCA = 90o - ABC
=> \(\frac{BCA}{2}=45^o-\frac{ABC}{2}=ACI\)
Δ ABH vuông tại H có: ABH + BAH = 90o
=> BAH = 90o - ABH
=> \(\frac{BAH}{2}=45^o-\frac{ABH}{2}=BAI\)
Lại có: IAC = BAC - BAI
=> IAC = 90o - (45o - \(\frac{ABH}{2}\))
=> IAC = 45o + \(\frac{ABH}{2}\)
Xét Δ AIC có: AIC + IAC + ICA = 180o (tổng 3 góc của Δ)
=> AIC + 45o + \(\frac{ABH}{2}\) + 45o - \(\frac{ABC}{2}\) = 180o
=> AIC + 90o = 180o
=> AIC = 180o - 90o = 90o (đpcm)

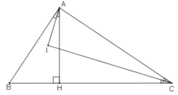
Ta có: AH⊥BC (gt) ⇒ ΔAHB vuông tại H
Trong tam giác vuông AHB ta có: ∠BHA = 90o
⇒ ∠B + ∠BAH = 90o (1)
Trong tam giác vuông ABC ta có: ∠BAC = 90o
⇒ ∠B + ∠C = 90o (2)
Từ (1) và (2) suy ra: ∠BAH = ∠C (3)
+) Vì AI là tia phân giác của góc BAC nên:
∠(BAI) = ∠(IAH) = 1/2.∠BAH (4)
Do CI là tia phân giác của góc ACB nên:
∠(ACI) = ∠(ICB) = 1/2.∠C (5)
+) Từ (3); (4) và (5) suy ra:
∠(BAI) = ∠(IAH) = ∠(ACI) = ∠(ICB)
+) Lại có:
∠BAI + ∠IAC = 90º
Suy ra: ∠ICA + ∠IAC = 90º
Trong ΔAIC có: ∠ICA+ ∠IAC = 90º
Vậy: ∠AIC = 90º.

Vẽ đường thẳng song song với AC và vuông góc với AB tài D và N ( góc NDA = 90 độ)
Xét tam giác NAD và tam giác NAH có :
góc DAN = góc NAH ( vì DN là tia p/g góc BAH)
AN cạnh chung
=> tam giác NAD = tam giác NAH ( ch-gn)
=> góc DNA = góc ANH ( hai góc tương ứng ) (1)
Mặt khác : góc DNA = góc NAC ( hai góc so le trong )
Kết hợp (1) => góc DNA = góc ANH = góc NAC => tam giác NCA cân tại C => NC =AC (3)
Xét tam giác NCI và tam giác ACI có:
NC =AC ( do (3))
CI cạnh chung
góc NCI = góc ICA ( CI là p/g góc BCA)
=> tam giác NCI = tam giác ACI ( c.g.c)
=> góc NIC = góc AIC ( hai góc tương ứng )
Mà góc NIC và góc AIC là cặp góc kề bù
=> góc NIC = góc AIC = 90 độ
