Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác ABC cân tại A. Gọi M là một điểm nằm trên cạnh BC sao cho MB<MC. Lấy điểm O trên đoạn thẳng AM. Chứng minh rằng góc AOB > góc AOC.

Bạn tự vẽ hình nha!
Ta có: BM<MC => góc BOM < góc MOC
Ta lại có: góc BOM + góc BOA = góc MOC + góc COA
mà góc BOM < góc MOC => góc BOA > góc COA

Cậu tham khảo ở đây ạ:
https://olm.vn/hoi-dap/detail/100073350231.html
hok tốt!!
^^

Trên nửa mặt phẳng bờ AC không chứa điểm B vẽ ^CAx=^OAB. Trên Ax lấy điểm I sao cho AO=AI
Nối I với O và C.
Xét \(\Delta\)AMB và \(\Delta\)AMC:
AB=AC
AM chung => ^MAB < ^MAC hay ^OAB < ^OAC
MB<MC
Mà ^OAB=^IAC => ^IAC < ^OAC
Xét \(\Delta\)AIC và \(\Delta\)AOC:
Cạnh AC chung
^IAC < ^OAC => IC < OC
AI=AO
Xét \(\Delta\)OCI có: IC < OC => ^OIC > ^IOC (1)
Ta có: Tam giác OAI: AO=AI => \(\Delta\)OAI cân tại A => ^AIO=^AOI (2)
Từ (1) và (2) => ^OIC+^AIO > ^IOC+^AOI => ^AIC > ^AOC (3)
Sau đó c/m \(\Delta\)AOB=\(\Delta\)AIC (c.g,c) => ^AIC=^AOB (4)
Từ (3) và (4) => ^AOB > ^AOC (đpcm).

Lời giải:
a.
Do tam giác $ABC$ cân tại $A$ nên $AB=AC$
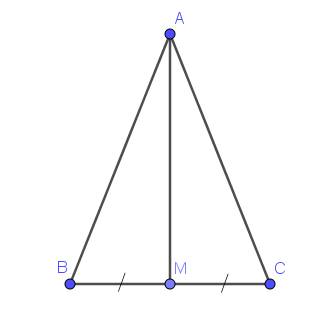
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{BAM}=\widehat{CAM}$. Mà $AM$ nằm giữa $AB, AC$ nên $AM$ là tia phân giác $\widehat{BAC}$
Cũng từ tam giác bằng nhau phần a suy ra:
$\widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$
$\Rightarrow \widehat{AMB}=180^0:2=90^0$
$\Rightarrow AM\perp BC$
c.
$AM\perp BC, M$ là trung điểm $BC$ nên $AM$ là đường trung trực của $BC$
$\Rightarrow$ mọi điểm $E\in AM$ đều cách đều 2 đầu mút B,C (theo tính chất đường trung trực)
$\Rightarrow EB=EC$
$\Rightarrow \triangle EBC$ cân tại $E$.