
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

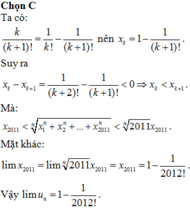

Ủa đề bài như này là sao bạn? Cho dãy x(k), nhưng lại đi tìm u(n)?
Đề bài có nghĩa là tìm giới hạn dãy:
\(u_n=\sqrt[n]{\left(\dfrac{1}{2!}\right)^n+\left(\dfrac{1}{2!}+\dfrac{2}{3!}\right)^n+...+\left(\dfrac{1}{2!}+\dfrac{2}{3!}+...+\dfrac{2011}{2012!}\right)^n}\)
Tìm được khá dễ dàng bằng cách sử dụng định lý kẹp

\(tan\left(x-\frac{\pi}{4}\right)=tan3x\)
\(\Leftrightarrow3x=x-\frac{\pi}{4}+k\pi\)
\(\Leftrightarrow x=-\frac{\pi}{8}+\frac{k\pi}{2}\)
Ủa mà kiểm tra với máy tính có mỗi đáp án D đúng (y như tự luận) lấy đâu ra 2 câu đều bằng 0 nhỉ?

bài này ta chia ra nhiều trường hợp nhé
TH1: bóng xanh rơi vào ô số 1
để thỏa mãn bài toán thì xác suất của TH này là : \(2^{-1}\left(2^{-2}+2^{-3}+...\right)\)
TH2: bóng xanh rơi vào ô số 2
để thỏa mãn bài toán thì xác suất của TH này là : \(2^{-2}\left(2^{-3}+2^{-4}+...\right)\)
........................................................................................................................................................
TH N : bóng xanh rơi vào ô số N
để thỏa mãn bài toán thì xác suất của TH này là :\(2^{-N}\left(2^{-\left(N+1\right)}+2^{-\left(N+2\right)}+...\right)\)
TỪ ĐÓ ta có thể thấy được xát suất để bóng đỏ được ném vào ô được đánh số cao hơn quả bóng xanh là : \(P=\left(2^{-1}+2^{-2}+...+2^{-N}\right)\left(2^{-\left(N+1\right)}+2^{-\left(N+2\right)}+...\right)+\left(2^{-1}.2^{-2}+2^{-2}.2^{-3}+...+2^{-\left(N-1\right)}.2^{-N}\right)\)
\(\Leftrightarrow P=\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{2^N}\right)\left(\frac{1}{2^{N+1}}+\frac{1}{2^{N+2}}+...\right)+\left(\frac{1}{2^3}+\frac{1}{2^5}+...+\frac{1}{2^{2N-1}}\right)\)
\(\Leftrightarrow P=\left(\frac{\frac{-1}{2}}{\frac{1}{2}-1}\right)\left(\frac{0}{0-1}\right)+\left(\frac{-\frac{1}{8}}{\frac{1}{8}-1}\right)=\frac{1}{7}\)

\(\lim\limits_{x\rightarrow1}\frac{x^{2016}+x-2}{\sqrt{2018x+1}-\sqrt{x+2018}}=\lim\limits_{x\rightarrow1}\frac{2016x^{2015}+1}{\frac{1009}{\sqrt{2018x+1}}-\frac{1}{2\sqrt{x+2018}}}=\frac{2017}{\frac{1009}{\sqrt{2019}}-\frac{1}{2\sqrt{2019}}}=2\sqrt{2019}\)
Để hàm liên tục tại \(x=1\)
\(\Rightarrow\lim\limits_{x\rightarrow1}f\left(x\right)=f\left(1\right)\Rightarrow k=2\sqrt{2019}\)
2.
\(\lim\limits_{x\rightarrow1}\frac{x^2+ax+b}{x^2-1}=\frac{1}{2}\Leftrightarrow\left\{{}\begin{matrix}a+b+1=0\\\lim\limits_{x\rightarrow1}\frac{2x+a}{2x}=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=-1\\\frac{a+2}{2}=\frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=0\end{matrix}\right.\) \(\Rightarrow S=1\)
3.
\(\lim\limits_{x\rightarrow1}\frac{\sqrt{x^2+x+2}-2+2-\sqrt[3]{7x+1}}{\sqrt{2}\left(x-1\right)}=\lim\limits_{x\rightarrow1}\frac{\frac{\left(x-1\right)\left(x+2\right)}{\sqrt{x^2+x+2}+2}-\frac{7\left(x-1\right)}{\sqrt[3]{\left(7x+1\right)^2}+2\sqrt[3]{7x+1}+4}}{\sqrt{2}\left(x-1\right)}\)
\(=\lim\limits_{x\rightarrow1}\frac{1}{\sqrt{2}}\left(\frac{x+2}{\sqrt{x^2+x+2}+2}-\frac{7}{\sqrt[3]{\left(7x+1\right)^2}+2\sqrt[3]{7x+1}+4}\right)\)
\(=\frac{1}{\sqrt{2}}\left(\frac{3}{4}-\frac{7}{12}\right)=\frac{\sqrt{2}}{12}\)
\(\Rightarrow a+b+c=1+12+0=13\)

Bạn có học thì suy nghĩ trước khi nói!Bạn muốn lời giải thì đây(mình lớp 10):
\(\sqrt{1+x}-\sqrt{x}=\dfrac{\left(\sqrt{1+x}-\sqrt{x}\right)\left(\sqrt{1+x}+\sqrt{x}\right)}{\sqrt{1+x}+\sqrt{x}}=\dfrac{1}{\sqrt{1+x}+\sqrt{x}}\)
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{1+x}-\sqrt{x}\right)=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{1}{\sqrt{1+x}+\sqrt{x}}\right)=0\)
Thành ĐạtNguyễn Huy TúĐức Minh.... æ CTV lo mà tag tên nhau vào mà giải quyết nhé t mà nói thì hơi quá
-Còn về bài này chả cần nâng cao tao đây làm 1 chốc là xong chỉ sợ động phải kiến thức m` chưa học thôi

Đường thẳng d thành đường thẳng d’ có phương trình được xác định bằng cách: Mỗi điểm M(x;y) ∈ d' là ảnh của 1 điểm M0(x0;y0) thuộc d qua phép tịnh tiến theo vecto u=(2;3), ta có:
\(\left\{{}\begin{matrix}M_0\left(x_0;y_0\right)\in d\\\overrightarrow{M_0M}=\overrightarrow{u}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0-2y_0+2=0\\x_0 =x-2\\y_0=y-3\end{matrix}\right.\)
\(\Rightarrow\left(x-2\right)-2\left(y-3\right)+2=0\Leftrightarrow x-2y+6=0\)
Đây là phương trình của d'