Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Bạn ghi lại đề, mẫu số ko rõ
2. \(=lim\left[-8n^6\left(1-\frac{4}{n^2}\right)^3\right]=-\infty.1=-\infty\)
3. Dãy số là CSC với \(\left\{{}\begin{matrix}u_1=-1\\d=3\end{matrix}\right.\) \(\Rightarrow u_n=-1+\left(n-1\right)3=3n-4\)
\(\Rightarrow lim\frac{3n-4}{5n+2020}=lim\frac{3-\frac{4}{n}}{5+\frac{2020}{n}}=\frac{3}{5}\)
4.
\(u_{n+1}=\frac{1}{2}u_n+\frac{3}{2}\Rightarrow u_{n+1}-3=\frac{1}{2}\left(u_n-3\right)\)
Đặt \(v_n=u_n-3\Rightarrow\left\{{}\begin{matrix}v_1=-2\\v_{n+1}=\frac{1}{2}v_n\end{matrix}\right.\)
\(\Rightarrow v_n\) là CSN với công bội \(\frac{1}{2}\Rightarrow v_n=-2.\frac{1}{2^{n-1}}\Rightarrow u_n=v_n+3=-\frac{1}{2^{n-2}}+3\)
\(\Rightarrow lim\left(u_n\right)=lim\left[-\frac{1}{2^{n-2}}+3\right]=3\)
5.
\(u_{n+1}=u_n+\frac{1}{2^n}\Rightarrow u_{n+1}+\frac{2}{2^{n+1}}=u_n+\frac{2}{2^n}\)
Đặt \(v_n=u_n+\frac{2}{2^n}\Rightarrow\left\{{}\begin{matrix}v_1=3\\v_{n+1}=v_n\end{matrix}\right.\)
\(\Rightarrow v_{n+1}=v_n=...=v_1=3\Rightarrow u_n=3-\frac{2}{2^n}\)
\(\Rightarrow u_{n-2}=3-\frac{2}{2^{n-2}}\Rightarrow lim\left(u_{n-2}\right)=lim\left(3-\frac{2}{2^{n-2}}\right)=3\)
Tính \(u_{n-2}\) hay \(u_n-2\) nhỉ? Ko dịch nổi nên đoán đại

\(u_2=\sqrt{2}\left(2+3\right)-3=5\sqrt{2}-3\)
\(u_3=\sqrt{\dfrac{3}{2}}.5\sqrt{2}-3=5\sqrt{3}-3\)
\(u_4=\sqrt{\dfrac{4}{3}}.5\sqrt{3}-3=5\sqrt{4}-3\)
....
\(\Rightarrow u_n=5\sqrt{n}-3\)
\(\Rightarrow\lim\limits\dfrac{u_n}{\sqrt{n}}=\lim\limits\dfrac{5\sqrt{n}-3}{\sqrt{n}}=5\)

* Xét tử số: Ta thấy 1, 2, 3, 4, ..., n là một dãy số thuộc cấp số cộng có n số hạng với
u 1 = 1 ; d= 1 .
Tổng n số hạng của cấp số cộng: S n = u 1 + u n n 2 = 1 + n n 2 .
* Xét mẫu số: Ta thấy 1 , 3 , 3 2 , 3 3 , ... , 3 n là một dãy số thuộc cấp số nhân có n + 1 số hạng với u 1 = 1 ; q = 3
Tổng (n+ 1) số hạng của cấp số nhân: S n + 1 = u 1 . 1 − q n + 1 1 − q = 1 − 3 n + 1 1 − 3 = 3 n + 1 − 1 2 .
⇒ u n = n 3 n + 1 − 1 = n 3.3 n − 1
Bằng quy nạp ta luôn có n < 2 n , ∀ n ∈ ℕ * và 3 n > 1 , ∀ n ∈ ℕ *
⇒ u n = n 3.3 n − 1 < n 3 n < 2 n 3 n = 2 3 n
Vì lim 2 3 n = 0 nên lim u n = 0.
Chọn đáp án A

\(U_n=\dfrac{an^2-1}{n^2+3}\)
\(=\dfrac{an^2+3a-3a-1}{n^2+3}\)
\(=a+\dfrac{-3a-1}{n^2+3}\)
Để dãy này là dãy tăng thì \(U_{n+1}>U_n\)
=>\(a+\dfrac{-3a-1}{\left(n+1\right)^2+3}>a+\dfrac{-3a-1}{n^2+3}\)
=>\(\dfrac{-3a-1}{\left(n+1\right)^2+3}>\dfrac{-3a-1}{n^2+3}\)
=>\(\dfrac{3a+1}{\left(n+1\right)^2+3}< \dfrac{3a+1}{n^2+3}\)(1)
TH1: 3a+1>0
=>a>-1/3
(1)=>\(\dfrac{1}{\left(n+1\right)^2+3}< \dfrac{1}{n^2+3}\)
=>\(\left(n+1\right)^2+3>n^2+3\)
=>\(\left(n+1\right)^2>n^2\)
=>\(n^2+2n+1-n^2>0\)
=>\(2n+1>0\)(luôn đúng với mọi n>=1)
TH2: 3a+1<0
=>a<-1/3
(2) trở thành \(\dfrac{1}{\left(n+1\right)^2+3}>\dfrac{1}{n^2+3}\)
=>\(\left(n+1\right)^2+3< n^2+3\)
=>\(n^2+2n+1-n^2< 0\)
=>2n+1<0
=>2n<-1
=>\(n< -\dfrac{1}{2}\)(loại)
Vậy: \(a>-\dfrac{1}{3}\)

\(\lim\left(1+\dfrac{-1}{2^n}\right)=1+0=1\Rightarrow a=1\)
\(\lim\left(\dfrac{n^5}{n^4-2n^3+1}-n\right)=\lim\left(\dfrac{n^5-n\left(n^4-2n^3+1\right)}{n^4-2n^3+1}\right)\)
\(=\lim\left(\dfrac{2n^4-n}{n^4-2n^3+1}\right)=\lim\left(\dfrac{2-\dfrac{1}{n^3}}{1-\dfrac{2}{n}+\dfrac{1}{n^4}}\right)=2\)

a: \(\dfrac{u_n}{u_{n-1}}=\dfrac{3^n}{2^{n+1}}:\dfrac{3^{n-1}}{2^n}\)
\(=\dfrac{3^n}{3^{n-1}}\cdot\dfrac{2^n}{2^{n+1}}=\dfrac{3}{2}>1\)
=>(un) là dãy tăng
c: ĐKXĐ: n>=1
\(u_n=\sqrt{n}-\sqrt{n-1}\)
\(=\dfrac{1}{\sqrt{n}+\sqrt{n-1}}\)
\(\dfrac{u_n}{u_{n-1}}=\dfrac{1}{\sqrt{n}+\sqrt{n-1}}:\dfrac{1}{\sqrt{n-1}+\sqrt{n-2}}\)
\(=\dfrac{\sqrt{n-1}+\sqrt{n-2}}{\sqrt{n-1}+\sqrt{n}}< 1\)
=>Đây là dãy số giảm
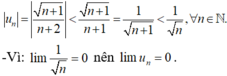
\(=\lim\limits\dfrac{n^2+an+5-n^2-1}{\sqrt{n^2+an+5}+\sqrt{n^2+1}}=\lim\limits\dfrac{an+4}{\sqrt{n^2+an+5}+\sqrt{n^2+1}}\)
\(=\lim\limits\dfrac{\dfrac{an}{n}+\dfrac{4}{n}}{\sqrt{\dfrac{n^2}{n^2}+\dfrac{an}{n^2}+\dfrac{5}{n^2}}+\sqrt{\dfrac{n^2}{n^2}+\dfrac{1}{n^2}}}=\dfrac{a}{1+1}=\dfrac{a}{2}\)
\(\lim\limits\left(u_n\right)=-1\Rightarrow\dfrac{a}{2}=-1\Rightarrow a=-2\)