Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Dựa vào định nghĩa và các tính chất của các số cộng và cấp số nhân.

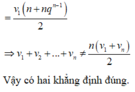


Đáp án D
Ta có
f n = n 2 + 1 + n 2 + 1 = n 2 + 1 2 + 2 n n 2 + 1 + n 2 + 1
= n 2 + 1 n 2 + 1 + 2 n + 1 = n 2 + 1 n 2 + 1 + 1 .
Do đó
f 2 n − 1 f 2 n = 2 n − 1 2 + 1 . 2 n 2 + 1 2 n 2 + 1 . 2 n + 1 2 + 1 = 2 n − 1 2 + 1 2 n + 1 2 + 1 .
Suy ra
u n = f 1 f 2 . f 3 f 4 . f 5 f 6 ... f 2 n − 1 f 2 n = 1 2 + 1 3 2 + 1 . 3 2 + 1 5 2 + 1 . 5 2 + 1 7 2 + 1 ... 2 n − 1 2 + 1 2 n + 1 2 + 1
⇒ u n = 2 2 n + 1 2 = 1 2 n 2 + 2 n + 1
⇒ lim n u n = lim n 2 n 2 + 2 n + 1 = 1 2 + 1 n + 1 n 2 = 1 2 .

Ta có:
3 n + 2 x n + 1 2 = 2 n + 1 x n + 1 2 + n + 4 ∀ n ≥ 21
⇔ 3 n + 2 x n + 1 2 = 2 n + 1 x n + 1 2 - 2 n + 1 + 3 n - 2 , ∀ n ≥ 21 ⇔ 3 n + 2 x n + 1 2 - 1 = 2 n + 1 x n 2 - 1
Đặt y n = x n 2 - 1 . Khi đó
y n + 1 = 2 3 . n + 1 n + 2 y n
Suy ra
y n + 1 = 2 n + 1 3 n + 2 . 2 n 3 n + 1 = 2 3 n + 1 . 1 n + 2 y 1
hay l i m y n = 0 . Vậy l i m x n = 1
Đáp án cần chọn là B

Chọn A.
Phương pháp:
Áp dụng công thức khai triển nhị thức Newton:
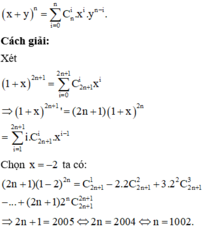

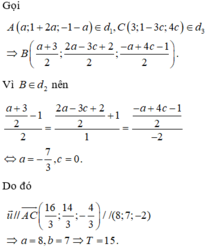
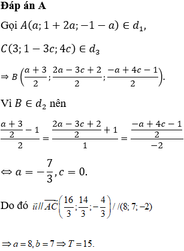
Đáp án là D