
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số hạng đầu của khai triển là u1 = u(1) = 13 = 1.
Số hạng cuối của khai triển là u5 = u(5) = 53 = 125.
Dãy số được viết dưới dạng khai triển là: 1; 8; 27; 64; 125.

a) Ta có số hạng tổng quát của dãy số \({u_n} = 5n + 1\;\left( {n\; \in {N^*}} \right)\).
b) Các số hạng của dãy số là: 6; 11; 16; 21; 26.
Số hạng đầu của dãy số là: 6 và số hạng cuối của dãy số là 26.

a) Năm số hạng đầu của dãy số là: \(u_1=1^2=1;u_2=2^2=4;u_3=3^2=9;u_4=4^2=16;u_5=5^2=25\).
Số hạng tổng quát của dãy số un là \(u_n=n^2\) với n ∈ ℕ.
b) Dạng khai triển của dãy số \(u_1=1,u_2=4,u_3=9,u_4=16,...u_n=n^2\) ...

a) Vì hàm số \(u\) xác định trên tập hợp các số nguyên dương
\(\mathbb{N}^{\text{∗
}}\) nên nó là một dãy số vô hạn.
b) Ta có:
\(u_1=1^3=1\\ u_2=2^3=8\\ u_3=3^3=27\\ u_4=4^3=64\\ u_5=5^3=125.\)



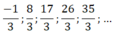

Ta thấy quy luật của dãy này là dãy các số nguyên tố liên tiếp tăng dần. Do đó \(u_8\) chính là số nguyên tố thứ 8 hay \(u_8=19\).