Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình gửi kèm
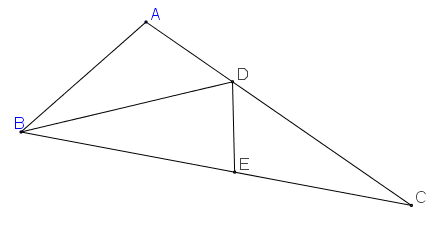 Nguồn: https://diendantoanhoc.net/topic/181822-frac1abfrac1acfrac1bc/
Nguồn: https://diendantoanhoc.net/topic/181822-frac1abfrac1acfrac1bc/

a: Xét ΔABC vuông tại A và ΔHBA vuông tạiH co
góc B chung
=>ΔABC đồng dạng vơi ΔHBA
=>BA/BH=BC/BA=AC/HA
=>BA^2=BH*BC
b: BI là phân giác
=>IA/IH=BA/BH=AC/HA
c: AK là phân giác của góc HAC
=>HK/KC=HA/AC=HI/IA
=>KI//AC

Lời giải:
a) Vì tam giác $ABC$ vuông tại $A$ nên:
$S_{ABC}=\frac{AB.AC}{2}$
Mặt khác: $S_{ABC}=\frac{AH.BC}{2}$
$\Rightarrow AB.AC=AH.BC$ (đpcm)
b) Áp dụng định lý Pitago cho tam giác $ABC$ vuông:
$BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
Áp dụng định lý Pitago cho tam giác $ABH$ vuông:
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
$\Rightarrow \frac{BD}{BD+DC}=\frac{BD}{BC}=\frac{3}{3+4}$
$\Rightarrow BD=BC.\frac{3}{7}=\frac{60}{7}$ (cm)
$DC=BC-BD=20-\frac{60}{7}=\frac{80}{7}$ (cm)

a:BC=căn 6^2+8^2=10cm
Xét ΔABC có AD là phân giác
nên BD/DC=AB/AC
=>BD/DC=3/4
=>BD/3=CD/4=(BD+CD)/(3+4)=10/7
=>BD=30/7cm
b: Xét ΔCED vuông tại E và ΔCAB vuông tại A có
góc C chung
=>ΔCED đồng dạng với ΔCAB
=>S CED/S CAB=(CD/CB)^2=(4/7)^2=16/49

Với tam giác ABC có góc A = \(90^o\)và góc B = \(30^o\)
=> Góc C = \(60^o\)
Gọi M là trung điểm của BC
Mà \(\Delta ABC\)có góc A = 90\(^o\)
=> AM = BM = CM \((\)định lý \()\)
=> Tam giác AMC cân tại M
Mà góc C = 60\(^o\)
=> \(\Delta ABC\)đều
=> AM = MC
Mà MC = \(\frac{1}{2}\)BC
Vậy : \(AC=\frac{1}{2}BC\)

Mình có làm bài này rồi, nhưng là chứng minh 2 chiều, bạn tự cắt ghép nhee :>


kết quả đây : http://123link.pw/DCO7IO
Nhớ cho đúng nha ^-^
Tam giác ABC có \(\left\{{}\begin{matrix}\widehat{A}=90^o\\\widehat{B}=30^o\end{matrix}\right.\)
\(\Rightarrow\Delta ABC\) là nửa tam giác đều
\(\Rightarrow AC=\dfrac{BC}{2}\)
mình không biết nửa tam giác đều là gì đâu bạn ạ