Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
c: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là phân giác của \(\widehat{BAC}\)
Bài 1:
a: XétΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔBAE=ΔBDE
b: ΔBAE=ΔBDE
=>EA=ED
Xét ΔEAF vuông tại A và ΔEDC vuông tại D có
EA=ED
\(\widehat{AEF}=\widehat{DEC}\)
Do đó: ΔEAF=ΔEDC
=>EF=EC
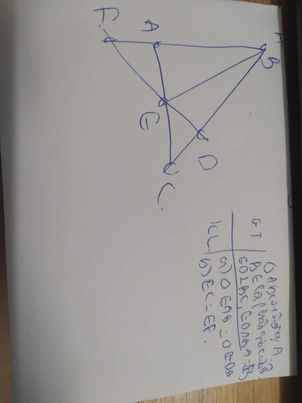


a, Vì AH là tia phân giác của ∠BAC
=> ∠BAH = ∠HAC = ∠BAC : 2
Xét △EAH vuong tại H và △FAH vuông tại H
Có: AH là cạnh chung
∠EAH = ∠FAH (cmt)
=> △EAH = △FAH (cgv-gn)
=> AE = AF (2 cạnh tương ứng)
Vì M là trung điểm của BC => MB = MC = BC/2
Qua C kẻ đường thẳng song song với AB cắt MF tại D
Ta có: CD // AB (cách vẽ) => ∠CDF = ∠AEF (2 góc đồng vị) (1) và ∠DCB = ∠ABC (2)
Xét △AEF có: AE = AF (cmt) => △AEF cân tại A => ∠AEF = ∠AFE (3)
Từ (1) và (3) => ∠AFE = ∠CDF hay ∠CFD = ∠CDF
Xét △CFD có: ∠CFD = ∠CDF (cmt) => △CFD cân tại C => CF = CD
Xét △CDM và △BEM
Có: ∠DCM = ∠EBM (cmt).
MC = MB (cmt)
∠CMD = ∠BME (2 góc đối đỉnh)
=> △CDM = △BEM (g.c.g)
=> CD = BE (2 cạnh tương ứng)
Mà CF = CD (cmt)
=> BE = CF
b, Ta có: AF = AC + CF (4) và AE = AB - BE (5)
Cộng 2 vế của (4) và (5) => AF + AE = AC + CF + AB - BE
Mà AF = AE và CF = BE
=> AE + AE = AC + AB
=> 2AE = AC + AB
=> AE = (AC + AB) : 2
Ta có: BE = AB - AE (6) và BE = CF mà CF = AF - AC => BE = AF - AC (7)
Cộng 2 vế của (6) và (7) => BE + BE = AB - AE + AF - AC => 2BE = AB - AC (AE = AF) => BE = (AB - AC) : 2
c, Xét △MBE có ∠MEA là góc ngoài của △ tại đỉnh E
=> ∠MEA = ∠EMB + ∠EBM => ∠AEF = ∠BME + ∠EBM => ∠AEF = ∠BME + ∠ABC
Xét △CFM có ∠MCA là góc ngoài của △ tại đỉnh C
=> ∠MCA = ∠CFM + ∠CMF => ∠ACB = ∠CFM + ∠CMF
Mà ∠CFM = ∠AEF (cmt) ; ∠CMF = ∠BME (2 góc đối đỉnh)
=> ∠ACB = ∠AEF + ∠BME
=> ∠ACB = ∠BME + ∠ABC + ∠BME
=> 2 . ∠BME + ∠ABC = ∠ACB
=> 2 . ∠BME = ∠ACB - ∠ABC
=> ∠BME = (∠ACB - ∠ABC) : 2

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
Suy ra: BA=BE và DA=DE
b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
SUy ra: AF=EC và DF=DC (1)
c: Ta có: BA+AF=BF
BE+EC=BC
mà BA=BE
và AF=EC
nên BF=BC(2)
Từ (1) và (2) suy ra BD⊥CF
bn có vt sai đề bài ko vậy