Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AD/BD=AM/MB=6/5
b: AE/EC=AM/MC=6/5
=>AD/BD=AE/EC
=>DE//BC
c: Để DE là đường trung bình thì D là trung điểm của AB, E là trung điểm của AC
Xét ΔAMB có
MD vừa la trung tuyến, vừa là phân giác
=>ΔMAB cân tại M
=>MA=MB=MC=1/2BC
=>ΔABC vuông tại A

a: AD/BD=AM/MB=6/5
b: AE/EC=AM/MC=6/5
=>AD/BD=AE/EC
=>DE//BC
c: Để DE là đường trung bình thì D là trung điểm của AB, E là trung điểm của AC
Xét ΔAMB có
MD vừa la trung tuyến, vừa là phân giác
=>ΔMAB cân tại M
=>MA=MB=MC=1/2BC
=>ΔABC vuông tại A

Xét △AMB và △DMC có:
\(\begin{matrix}MA=MD\left(gt\right)\\\hat{AMB}=\hat{CMD}\left(đối\text{ }đỉnh\right)\\MB=MC\left(gt\right)\end{matrix}\) ⇒ \(\Delta AMB=\Delta DMC\left(c.g.c\right)\Rightarrow\hat{ABM}=\hat{DCM}\left(1\right)\)
- Ta có: \(AM=\dfrac{1}{2}BC=MB\) ⇒ △AMB cân tại M \(\Rightarrow\hat{MAB}=\hat{MBA}\left(2\right)\)
Mặt khác: \(\hat{MAB}=\hat{MDC}\left(3\right)\)
Từ (1), (2) và (3) \(\Rightarrow\hat{MCD}=\hat{MDC}\left(4\right)\)
Mà AF // BC \(\Rightarrow\hat{AFC}=\hat{MCD}\left(đv\right)\left(5\right)\)
Từ (4) và (5) \(\Rightarrow\hat{AFC}=\hat{MDC}\) hay △ADF cân tại A (đpcm).

a: Xét ΔABC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
AM=BC/2=6,5cm
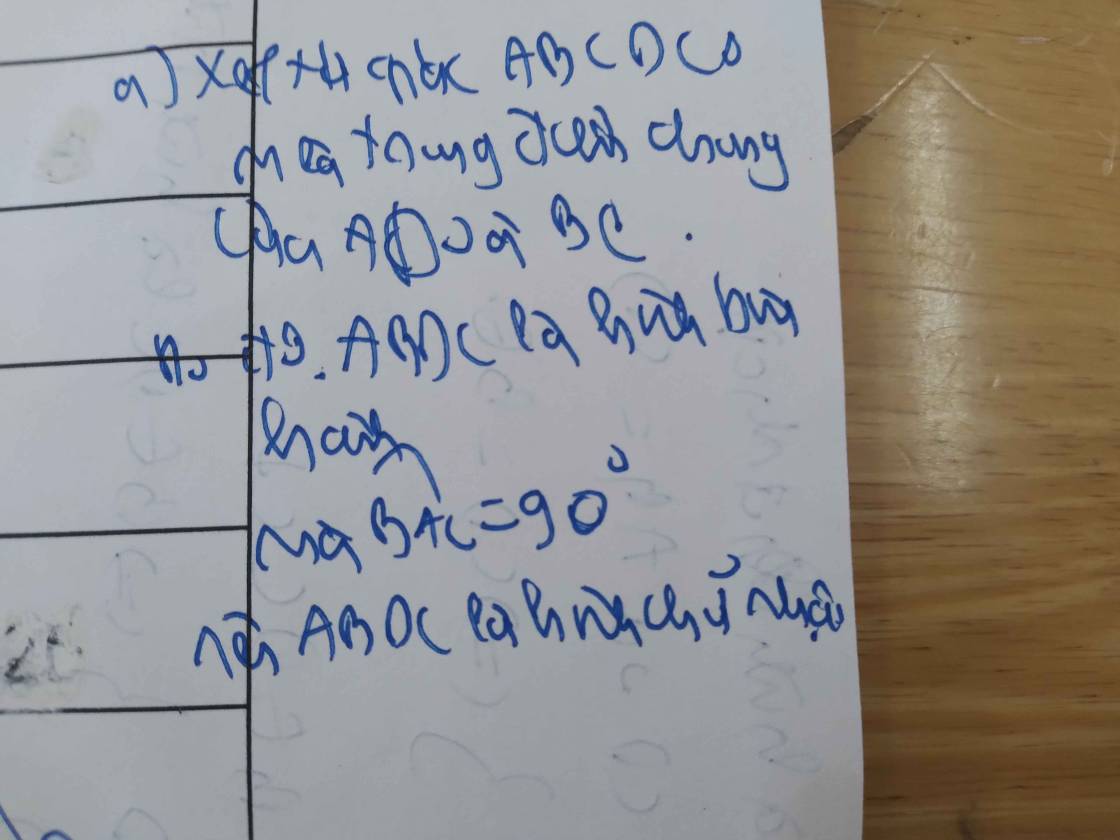
b: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
nên ADMElà hình chữ nhật
=>AM=DE
c: Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó: D là trung điểm của BA
Xét ΔABC có
M là trung điểm của BC
ME//AB
Do do: E là trung điểm của AC
Xét ΔABC có D,E lần lượt là trung điểm của AB,AC
nên DE là đường trung bình
=>DE//BC
=>BDEC là hình thang

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=3^2+4^2=25\)
=>BC=5(cm)
b: Xét ΔABC có MN//BC
nên \(\dfrac{AM}{AB}=\dfrac{MN}{BC}\)
=>\(\dfrac{MN}{5}=\dfrac{1.2}{3}=\dfrac{2}{5}\)
=>MN=2(cm)
c: Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
=>\(\dfrac{BD}{3}=\dfrac{CD}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{BC}{7}=\dfrac{5}{7}\)
=>\(\dfrac{BD}{3}=\dfrac{5}{7};\dfrac{CD}{4}=\dfrac{5}{7}\)
\(\dfrac{BD}{3}=\dfrac{5}{7}\)
=>\(BD=\dfrac{5}{7}\cdot3=\dfrac{15}{7}\left(cm\right)\)
d: \(\dfrac{CD}{4}=\dfrac{5}{7}\)
=>\(CD=\dfrac{5}{7}\cdot4=\dfrac{20}{7}\left(cm\right)\)
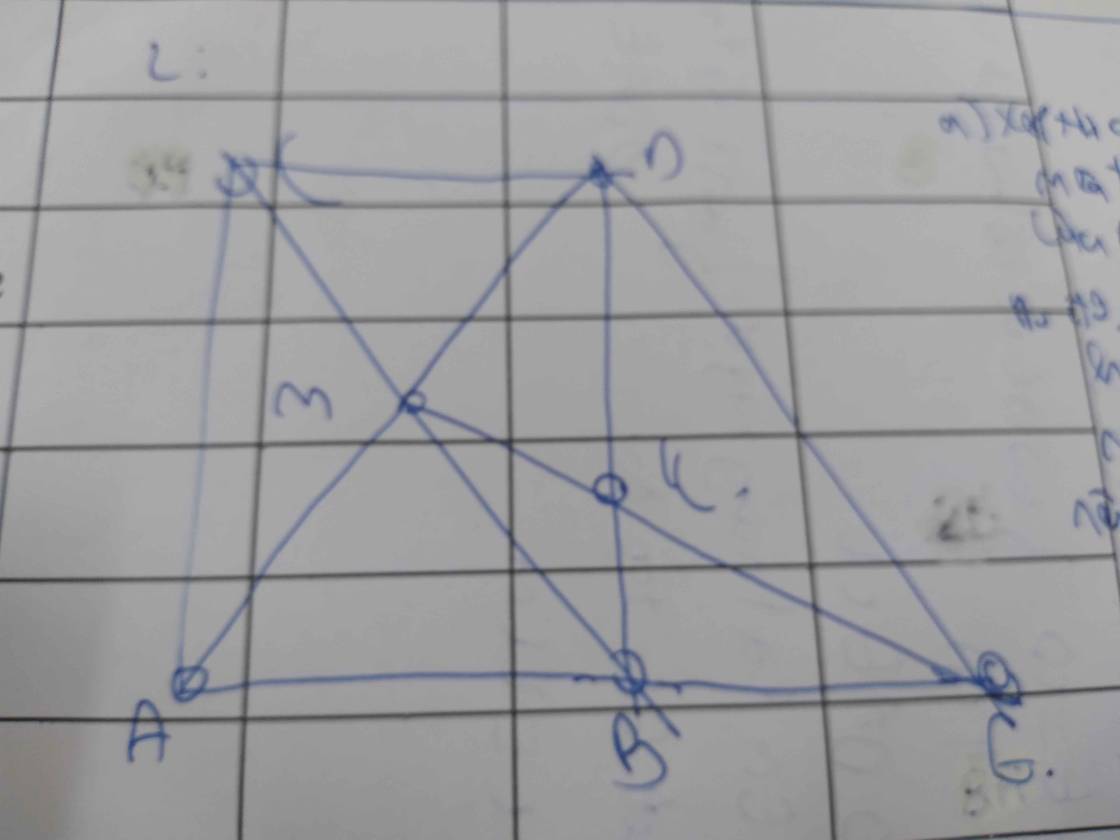

a: Xét ΔABM có DN//BM
nên DN/BM=AD/AB
hay DN/CM=AD/AB(1)
Xét ΔACM có NE//MC
nên NE/MC=AE/AC(2)
Xét ΔABC có DE//BC
nên AD/AB=AE/AC(3)
Từ (1), (2) và (3) suy ra ND=NE
hay N là trung điểm của DE
=>MN là đường trung bình
b: Xét ΔNMD có \(\widehat{NMD}=\widehat{NDM}\left(=\widehat{DMB}\right)\)
nên ΔNMD cân tại N
Xét ΔMNE có NE=NM
nên ΔMNE cân tại N
Xét ΔMDE có
NM là đường trung tuyến
MN=DE/2
Do đó: ΔMDE vuông tại M