NT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
15 tháng 8 2018
Theo định lý tổng ba góc trong tam giác ABC, ta có:
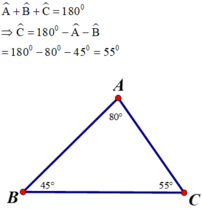
Cạnh đối diện góc B là AC
Cạnh đối diện góc C là AB
Cạnh đối diện góc A là BC
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Vì 450 < 550 < 800 hay B̂ < Ĉ < Â ⇒ AC < AB < BC.
GB
1
23 tháng 10 2021
Xét ΔABC có góc B=góc C
nên ΔABC cân tại A
mà AD là đường phân giác
nên AD là đường cao
ND
4
24 tháng 4 2020
3) Cho tam giác ABC cân tại B, B̂ = 600 thì số đo 𝐴̂ là:
A. 500
B. 550
C. 700
D. Ba câu trên đều sai
nếu cần giải thik thì bảo vs mik nhé!! hok tốt!!
LK
1
JS
30 tháng 3 2020
a) Xét △BDA và △BDE có:
\(\widehat{BAD}=\widehat{BED}=90^0\)
BD : cạnh chung
\(\widehat{ABD}=\widehat{EBD}\left(g.t\right)\)
⇒ △BDA = △BDE (đpcm)
b) Ta có: △BDA = △BDE
⇒ BA = BC (Hai cạnh tương ứng)
Vậy △ABE là tam giác cân tại B vì BA = BC.
c) Ta có: \(\widehat{ABC}=60^0\)
\(\Rightarrow\widehat{BCA}=30^0\)
Mà \(\widehat{ABD}=\widehat{EBD}=\frac{1}{2}\widehat{ABC}=30^0\)
\(\Rightarrow\widehat{BCA}=\widehat{EBD}\)
⇒ △BCD cân tại D.
Mà DE là đường cao của △BCD.
⇒ DE cũng là đường trung tuyến.
⇒ BE = EC = 5 (Vì AB = BE = 5)
⇒ BC = 5 + 5 = 10(cm)
Chúc bạn học tốt@@
3 tháng 2 2022
Xét ΔABC vuông tại A có \(\cos B=\dfrac{AB}{BC}\)
=>6/BC=1/2
=>BC=12(cm)
=>\(AC=6\sqrt{3}\left(cm\right)\)
Xét ΔABC có CD là đường phân giác
nên AD/AC=DB/BC
\(\Leftrightarrow\dfrac{AD}{6\sqrt{3}}=\dfrac{DB}{12}\)
mà AD+DB=6
nên Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{AD}{6\sqrt{3}}=\dfrac{DB}{12}=\dfrac{AD+DB}{6\sqrt{3}+12}=\dfrac{6}{12+6\sqrt{3}}=2-\sqrt{3}\)
Do đó: \(AD=12\sqrt{3}-18\left(cm\right);DB=24-12\sqrt{3}\left(cm\right)\)