Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Sửa đề: Chứng minh ΔABM=ΔACM
Xét ΔABM và ΔACM có
AB=AC(gt)
AM chung
BM=CM(M là trung điểm của BC)
Do đó: ΔABM=ΔACM(c-c-c)
Ta có: AB=AC(gt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: MB=MC(M là trung điểm của BC)
nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của BC
b) Xét ΔABM vuông tại M và ΔDCM vuông tại M có
MB=MC(M là trung điểm của BC)
AM=DM(gt)
Do đó: ΔABM=ΔDCM(hai cạnh góc vuông)
⇒\(\widehat{ABM}=\widehat{DCM}\)(hai góc tương ứng)
mà \(\widehat{ABM}\) và \(\widehat{DCM}\) là hai góc ở vị trí so le trong
nên AB//CD(Dấu hiệu nhận biết hai đường thẳng song song)

a, xét hai tam giác ABM và ACM có AB=AC, MB=MC, AM chung \(\Rightarrow\) ABM=ACM (c.c.c)
b, AB=AC nên ABC là tam giác cân, M là trung điểm BC nên AM vuông góc với BC
c,xét 2 tam giác AEH và CEM có EA=EC, EM=EH, góc MEC= góc HEA nên hai tam giác đó bằng nhau (c.g.c)
d, theo câu c đã có tam giác AEH=CEM nên góc AHE= góc CME. Hai góc này ở vị trí so le nên AH // BC (1)
tiếp tục xét 2 tam giác DKA và DMB, có góc KDA=DBM, DK = DM. Mặt khác ta thấy DMEA là hinhf bình hành nên ME=AD=DB ( do ME cũng là đường trung bình của ABC)
nên suy ra tam giác DKA=DMB suy ra góc AKD=BMD, hai góc này ở vị trí so le nên AK// BC(2)
Từ 1 và 2 suy ra AH và AK cùng nằm trên 1 đường thẳng hay K,H,A thẳng hàng...

a: Xét ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
=>góc MAB=góc MDC
=>AB//DC
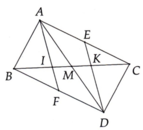
b: Xét ΔKMB và ΔFMC có
góc MBK=góc MCK
MB=MC
góc KMB=góc FMC
=>ΔKMB=ΔFMC
=>MK=MF
=>M là trung điểm của KF

a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM

a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM
câu a có bạn bên trên là rồi nên mình sẽ làm câu b nha bạn ^^
b) Vì tam giác ABC cân có MA phân giác => MA vuông BC và M trung điểm BC. Vì MA = MD nên M trung điểm AD.
Xét tứ giác ABDC có M trung điểm AD và BC => hình bình hành
=> AB = CD, AB // CD

a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM

a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM


a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM