Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đồng chí tự vẽ hình nhé.
Kẻ \(AD\perp BC=\left\{D\right\}\)
a, \(\Delta ABD\)có: \(\widehat{ADB}=90^o\)
\(\Rightarrow AD=AB.\sin B\Leftrightarrow AD=16.\sin30=8\sqrt{3}\left(cm\right)\)
\(\Delta ABD\)có: \(\widehat{ADB}=90^o\)
\(\Rightarrow AB^2=AD^2+BD^2\)(định lý Py-ta-go)
hay \(16^2=\left(8\sqrt{3}\right)^2+BD^2\)
\(BD^2=64\)
\(BD=8\left(cm\right)\)
\(\Delta ADC\)có: \(\widehat{ADC}=90^o\)
\(\Rightarrow AC^2=AD^2+CD^2\)(định lý Py-ta-go)
hay \(14^2=\left(8\sqrt{3}\right)^2+CD^2\)
\(CD^2=4\)
\(CD=2\left(cm\right)\)
Ta có: \(BC=CD+BD=2+8=10\left(cm\right)\)
b, \(S_{\Delta ABC}=\frac{AD.BC}{2}=\frac{8\sqrt{3}.10}{2}=40\sqrt{3}\left(cm^2\right)\)
Thật sự tui không biết mình có làm đúng không, sai thì nhớ bảo nhá

Kẻ CH vuông góc với AB tại H . Đặt HB = x ( 0 < x < 16 )
Xét tam giác vuông HBC có : tg 60 = \(\frac{HC}{HB}\Rightarrow HC=tg60^0.HB=x\sqrt{3}\)
Áp dụng định lí Pytago cho tam giác vuông AHC ta có : \(AC^2=AH^2+HC^2\)
\(14^2=\left(16-x\right)^2+3x^2\)
\(\Leftrightarrow x^2-8x+15=0\)
<=> x1 = 3 (tm) và x2 = 5 (tm )
Xét với x = 3 ta có : HB = 3 ; HC = \(3\sqrt{3}\). Áp dụng định lí Pytago cho tam giác vuông HBC ta có :
\(BC=\sqrt{HB^2+HC^2}=\sqrt{3^2+3.3^2}=6\)(cm )
Xét với x = 5 ta có : HB = 5 ; HC = \(5\sqrt{3}\); \(BC=\sqrt{HB^2+HC^2}=\sqrt{5^2+3.5^2}=10\)( cm )
Diện tích tam giác ABC là :
Với HC = 3 căn 3 ta có : HC. AB/2 = 24 căn 3 ( cm2)
với HC = 5 căn 3 ta có : HC.AB = 40 căn 3 ( cm 2 )

cosB=(16^2+BC^2-14^2)/(2*16*BC)
=>BC^2+60=32*BC*cos40
=>BC=21,76cm
S ABC=1/2*21,76*16*sin40=111,90cm2

a) Kẻ đường cao AH
Tam giác AHB vuông tại H , áp dụng HTL cạnh và góc
=> AH = AB .sin 60 = 8 căn 3
=> BH = AB.cos60 = 16.1/2 = 8
TAm giác AHC vuông tại H ; ÁP dụng py ta go tính HC
BC = BH + HC= 8+ \(\sqrt{3}\)=9,732

làm bừa thui,ai tích mình mình tích lại
Số số hạng là :
Có số cặp là :
50 : 2 = 25 ( cặp )
Mỗi cặp có giá trị là :
99 - 97 = 2
Tổng dãy trên là :
25 x 2 = 50
Đáp số : 50

bài giải
chú ý dấu nhân viết tắt bằng kí hiệu *
BC là
60+(12-8)=64 (cm)
diện tích hình tam giác ABC là
(12+8+64):2=42 (cm)
đáp số 42 cm
chúc bạn làm bài tập tốt
dippi
bạn cute thật đó ><

Kẻ đường cao AH ứng với BC
Trong tam giác vuông ACH:
\(sinC=\dfrac{AH}{AC}\Rightarrow AH=AC.sinC\)
\(cosC=\dfrac{CH}{AC}\Rightarrow CH=AC.cosC\)
Trong tam giác vuông ABH:
\(tanB=\dfrac{AH}{BH}\Rightarrow BH=\dfrac{AH}{tanB}=\dfrac{AC.sinC}{tanB}\)
Do đó:
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AH\left(BH+CH\right)=\dfrac{1}{2}.4,5.sin55^0.\left(\dfrac{4,5.sin55^0}{tan60^0}+4,5.cos55^0\right)\approx8,68\left(cm^2\right)\)
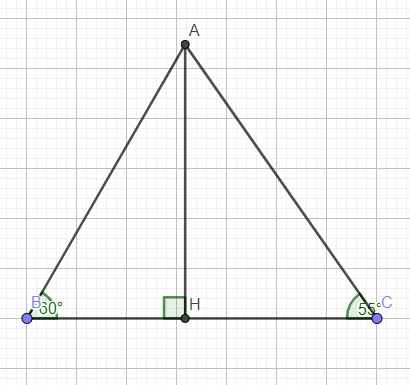
Lời giải:
Kẻ đường cao $AH$ $(H\in BC)$
Xét tam giác vuông $HAB$:
$\frac{BH}{AB}=\cos B\Rightarrow BH=\cos B.AB=\cos 60.14=7$ (cm)
$AH^2=AB^2-BH^2=14^2-7^2=147$ (cm) theo định lý Pitago
$CH=\sqrt{AC^2-AH^2}=\sqrt{16^2-147}=\sqrt{109}$ (cm)
$BC=BH+CH=7+\sqrt{109}$ (cm)
b)
$S_{ABC}=\frac{AH.BC}{2}=\frac{\sqrt{147}(7+\sqrt{109})}{2}$ (cm2)
Hình vẽ: