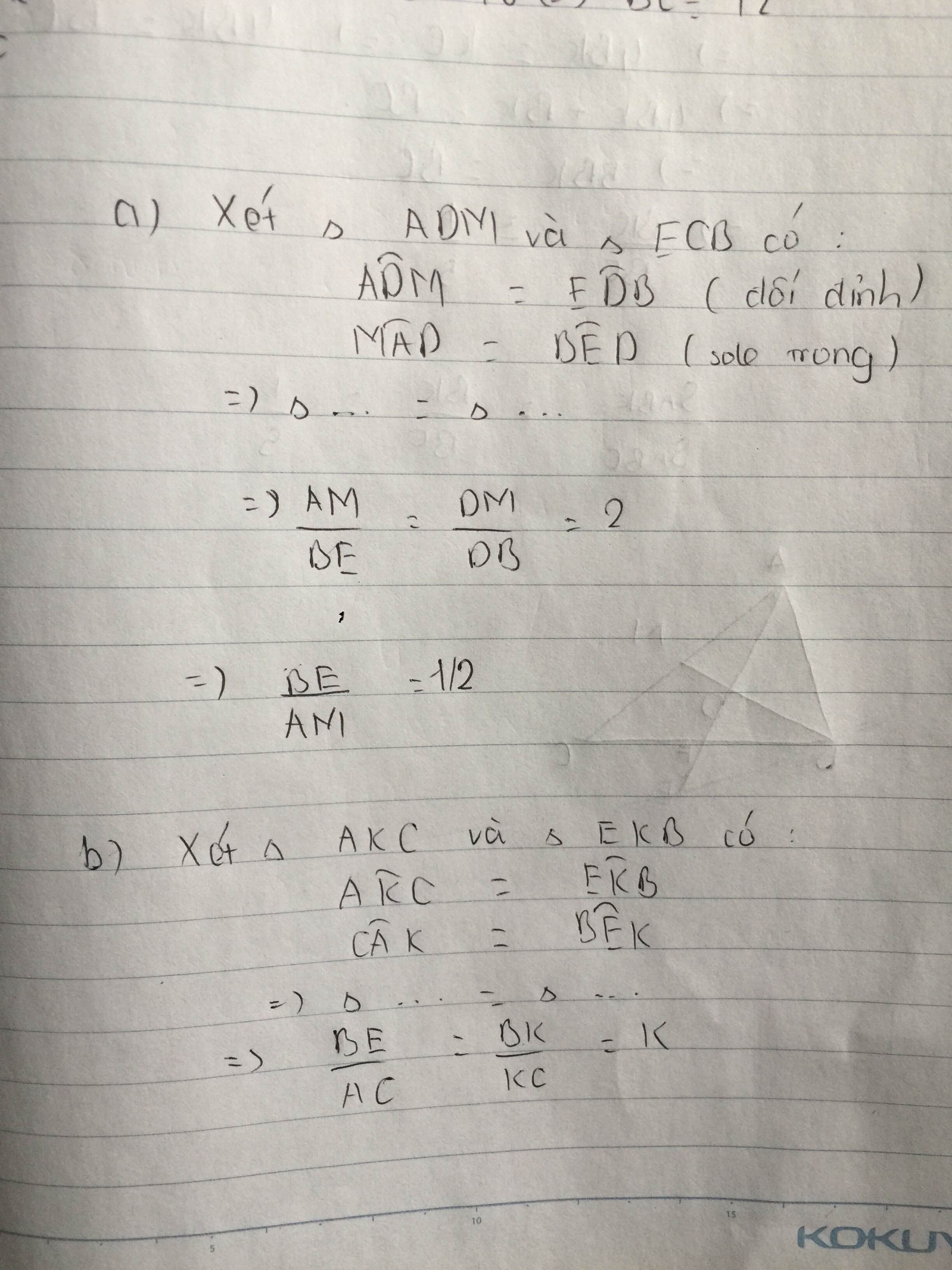Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a) Xét tam giác $HEA$ và $HDB$ có:
$\widehat{HEA}=\widehat{HDB}=90^0$
$\widehat{EHA}=\widehat{DHB}$ (đối đỉnh)
$\Rightarrow \triangle HEA\sim \triangle HDB$ (g.g)
b) Xét tam giác $CKD$ và $CDA$ có:
$\widehat{C}$ chung
$\widehat{CKD}=\widehat{CDA}=90^0$
$\Rightarrow \triangle CKD\sim \triangle CDA$ (g.g)
$\Rightarrow \frac{CK}{CD}=\frac{CD}{CA}\Rightarrow CD^2=CK.CA$ (đpcm)
c) Xét tam giác $ADK$ và $DCK$ có:
$\widehat{AKD}=\widehat{DKC}=90^0$
$\widehat{ADK}=\widehat{DCK}$ (cùng phụ $\widehat{KDC}$)
$\Rightarrow \triangle ADK\sim \triangle DCK$ (g.g)
$\Rightarrow \frac{AD}{DC}=\frac{DK}{CK}\Leftrightarrow \frac{FD}{2DC}=\frac{DK}{2CN}$
$\Rightarrow \frac{FD}{DC}=\frac{DK}{CN}$
Tam giác $FDK$ và $DCN$ đồng dạng với nhau do:
$\frac{FD}{DC}=\frac{DK}{CN}$ (cmt)
$\widehat{FDK}=\widehat{DCN}$ (cùng phụ $\widehat{KDC}$)
$\Rightarrow \frac{DFK}=\widehat{CDN}$
$\Rightarrow \widehat{DFK}+\widehat{FDN}=\widehat{CDN}+\widehat{FDN}$
$\Leftrightarrow 180^0-\widehat{FSD}=\widehat{FDC}=90^0$
$\Rightarrow \widehat{FSD}=90^0$ nên ta có đpcm.

a: Xét ΔDBE và ΔDMA có
góc DBE=góc DMA
góc BDE=góc MDA
=>ΔDBE đồng dạng vơi ΔDMA
=>BE/MA=DB/DM=1/3
=>BE=1/3MA=1/3*1/2AC=1/6AC
b: BE//AC
=>BK/KC=BE/AC=1/4
=>BK/BC=1/5

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
b: Xét ΔADM có
AE là đường cao
AE là đường trung tuyến
Do đó: ΔADM cân tại A
=>AD=AM
ΔADM cân tại A
mà AE là đường cao
nên AE là phân giác của \(\widehat{DAM}\left(1\right)\)
Xét ΔADN có
AF là đường cao
AF là đường trung tuyến
Do đó: ΔADN cân tại A
=>AD=AN
ΔADN cân tại A
mà AF là đường cao
nên AF là phân giác của \(\widehat{DAN}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{MAN}=\widehat{MAD}+\widehat{NAD}\)
\(=2\left(\widehat{EAD}+\widehat{FAD}\right)\)
\(=2\cdot\widehat{FAE}=2\cdot90^0=180^0\)
=>M,A,N thẳng hàng(3)
AM=AD
AN=AD
Do đó: AM=AN(4)
Từ (3) và (4) suy ra A là trung điểm của MN
c: Xét ΔADB và ΔAMB có
AD=AM
\(\widehat{DAB}=\widehat{MAB}\)
AB chung
Do đó: ΔADB=ΔAMB
=>\(\widehat{AMB}=\widehat{ADB}=90^0\)
=>BM\(\perp\)MN(5)
Xét ΔADC và ΔANC có
AD=AN
\(\widehat{DAC}=\widehat{NAC}\)
AC chung
Do đó: ΔADC=ΔANC
=>\(\widehat{ANC}=\widehat{ADC}=90^0\)
=>CN\(\perp\)NM(6)
Từ (5) và (6) suy ra BM//CN
Xét tứ giác BMNC có
BM//CN
BM\(\perp\)MN
Do đó: BMNC là hình thang vuông