
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A(x)=F(x)-G(x)
=1+x+x^2+...+x^100-x^2-x^4-...-x^100
=1+x+x^3+...+x^99
Số số lẻ từ 1 đến 99 là (99-1):2+1=50(số)
A(-1)=1+(-1)+(-1)^3+...+(-1)^99
=1-50*1=1-50=-49

Thay x = -1 và đa thức, ta có:
(-1)2 + (-1)4 + (-1)6 + … + (-1)100 = 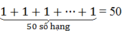
Vậy giá trị đa thức bằng 50 tại x = -1.

Ta đặt và thực hiện phép tính P(x) + Q(x) và P(x) – Q(x) có
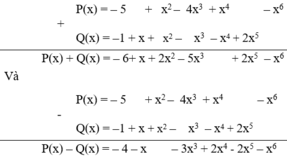
Vậy: P(x) + Q(x) = – 6 + x + 2x2 – 5x3 + 2x5 – x6
P(x) – Q(x) = – 4 – x – 3x3 + 2x4 - 2x5 – x6

P(x) = 3x2 – 5 + x4 – 3x3 – x6 – 2x2 – x3
= – x6 + x4 + (– 3x3 – x3) + (3x2 – 2x2) – 5
= – x6 + x4 – 4x3 + x2 – 5.
= – 5+ x2 – 4x3 + x4 – x6
Và Q(x) = x3 + 2x5 – x4 + x2 – 2x3 + x –1
= 2x5 – x4 + (x3 – 2x3) + x2 + x –1
= 2x5 – x4 – x3 + x2 + x –1.
= –1+ x + x2 – x3 – x4 + 2x5

a) \(M\left(x\right)=-x^6+x^4-4x^3+x^2-5\)
\(N\left(x\right)=2x^5-x^4-x^3+x^2+x-1\)
b)\(M\left(x\right)+N\left(x\right)=-x^6+x^4-4x^3+x^2-5+2x^5-x^4-x^3+x^2+x-1\) \(=-x^6+2x^5-5x^3+2x^2+x-6\)
Vậy...
\(M\left(x\right)-N\left(x\right)=-x^6+x^4-4x^3+x^2-5-\left(2x^5+x^4-x^3+x^2-x-1\right)\)\(=-x^6+x^4-4x^3+x^2-5-2x^5+x^4+x^3-x^2+x+1\) \(=-x^6-2x^5+2x^4-3x^3+x-4\) Vậy...
c) -N(x)+M(x)=.........

a. M(x) = 3x2- 5+ x4- 3x3- x6- 2x2- x3
= - 5+ (3x2- 2x2)+(-3x3- x3)+ x4- x6
= - 5 +x2+ (-4x3) +x4 -x6
N(x) = x3 + 2x5 -x4 +x2 -2x3 +x-1
= -1+x+x2+(x3- 2x3) -x4+ 2x5
= -1+ x+ x2+ (-x3) -x4+ 2x5
b. M(x) +N(x)= (- 5 +x2 -4x3 +x4 -x6) + (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1+ x+ x2 -x3 -x4+ 2x5
= (-5-1) + x +( x2 +x2) +(-4x3-x3) +(x4-x4) +2x5 -x6
= -6 +x +2x2 +(-5x3) +0 +2x5-x6
= -6 +x +2x2 +(-5x3) +2x5-x6
M(x) -N(x)= (- 5 +x2 -4x3 +x4 -x6) - (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1-x -x2 +x3 +x4 -2x5
= (-5-1) +x +(x2-x2) +(-4x3+x3) +(x4+x4) -2x5 -x6
= -6 +x +0 +(-3x3) +2x4 -2x5 -x6
= -6 +x +(-3x3) +2x4 -2x5 -x6

a. M(x) = 3x2- 5+ x4- 3x3- x6- 2x2- x3
= - 5+ (3x2- 2x2)+(-3x3- x3)+ x4- x6
= - 5 +x2+ (-4x3) +x4 -x6
N(x) = x3 + 2x5 -x4 +x2 -2x3 +x-1
= -1+x+x2+(x3- 2x3) -x4+ 2x5
= -1+ x+ x2+ (-x3) -x4+ 2x5
b. M(x) +N(x)= (- 5 +x2 -4x3 +x4 -x6) + (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1+ x+ x2 -x3 -x4+ 2x5
= (-5-1) + x +( x2 +x2) +(-4x3-x3) +(x4-x4) +2x5 -x6
= -6 +x +2x2 +(-5x3) +0 +2x5-x6
= -6 +x +2x2 +(-5x3) +2x5-x6
M(x) -N(x)= (- 5 +x2 -4x3 +x4 -x6) - (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1-x -x2 +x3 +x4 -2x5
= (-5-1) +x +(x2-x2) +(-4x3+x3) +(x4+x4) -2x5 -x6
= -6 +x +0 +(-3x3) +2x4 -2x5 -x6
= -6 +x +(-3x3) +2x4 -2x5 -x6

a. M(x) = 3x2- 5+ x4- 3x3- x6- 2x2- x3
= - 5+ (3x2- 2x2)+(-3x3- x3)+ x4- x6
= - 5 +x2+ (-4x3) +x4 -x6
N(x) = x3 + 2x5 -x4 +x2 -2x3 +x-1
= -1+x+x2+(x3- 2x3) -x4+ 2x5
= -1+ x+ x2+ (-x3) -x4+ 2x5
b. M(x) +N(x)= (- 5 +x2 -4x3 +x4 -x6) + (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1+ x+ x2 -x3 -x4+ 2x5
= (-5-1) + x +( x2 +x2) +(-4x3-x3) +(x4-x4) +2x5 -x6
= -6 +x +2x2 +(-5x3) +0 +2x5-x6
= -6 +x +2x2 +(-5x3) +2x5-x6
M(x) -N(x)= (- 5 +x2 -4x3 +x4 -x6) - (-1+ x+ x2 -x3 -x4+ 2x5)
= - 5 +x2 -4x3 +x4 -x6 -1-x -x2 +x3 +x4 -2x5
= (-5-1) +x +(x2-x2) +(-4x3+x3) +(x4+x4) -2x5 -x6
= -6 +x +0 +(-3x3) +2x4 -2x5 -x6
= -6 +x +(-3x3) +2x4 -2x5 -x6

* f(x) = x2 + 2x3− 7x5 − 9 − 6x7 + x3 + x2 + x5 − 4x2 + 3x7
= (x2+ x2 – 4x2)+ (2x3 + x3 ) - (7x5 - x5 ) – 9 – (6x7 – 3x7)
= - 2x2 + 3x3 – 6x5 – 9 – 3x7
Sắp xếp theo thứ tự tăng của biến: f(x) = −9 − 2x2 + 3x3 − 6x5 − 3x7
* g(x) = x5 + 2x3 − 5x8 − x7 + x3 + 4x2 -5x7 + x4 − 4x2 − x6 – 12
= x5+ (2x3 + x3) - 5x8 – (x7+ 5x7) + (4x2 – 4x2 ) + x4 – x6 – 12
= x5 + 3x3 – 5x8 – 6x7 + x4 – x6 – 12
Sắp xếp theo thứ tự tăng của biến: g(x) = −12 + 3x3 + x4 + x5 – x6 − 6x7− 5x8
* h(x) = x + 4x5 − 5x6 − x7 + 4x3 + x2 − 2x7 + x6 − 4x2 − 7x7 + x.
= (x+ x) +4x5 – (5x6 – x6)- (x7 + 2x7+ 7x7) + 4x3+ (x2 – 4x2)
= 2x + 4x5 - 4x6 – 10x7 + 4x3 -3x2
Sắp xếp theo thứ tự tăng của biến: h(x) = 2x − 3x2 + 4x3 + 4x5 − 4x6 − 10x7
\(M\left(x\right)=1+\left(-1\right)+\left(-1\right)^2+\left(-1\right)^3+\left(-1\right)^4+...+\left(-1\right)^{100}\)
\(=1+\left(-1\right)+\left(-1\right)^2+\left(-1\right)^3+\left(-1\right)^4+\left(-1\right)^5+...+\left(-1\right)^{98}+\left(-1\right)^{99}+\left(-1\right)^{100}\)
\(=1+\left(-1\right)+1+\left(-1\right)+1+\left(-1\right)+...+1+\left(-1\right)+1\)
\(=1\)
\(N\left(-1\right)=\left(-1\right)^2+\left(-1\right)^4+\left(-1\right)^6+\left(-1\right)^8+...+\left(-1\right)^{100}\)
\(=1+1+1+1+...+1\)
\(=50.1=50\)
\(M\left(-1\right)-N\left(-1\right)=1-50=-49\)
thak nhìu nhắm :D