Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ P(x) chia hết cho x + 1
⇔ P(-1) = 0
⇔ m . ( - 1 ) 3 + ( m – 2 ) ( - 1 ) 2 – ( 3 n – 5 ) . ( - 1 ) – 4 n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P(x) chia hết cho x – 3
⇔ P(3) = 0
⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình :
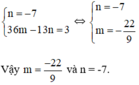

+ P(x) chia hết cho x + 1
⇔ P(-1) = 0
⇔ m.(-1)3 + (m – 2)(-1)2 – (3n – 5).(-1) – 4n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P(x) chia hết cho x – 3
⇔ P(3) = 0
⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình :
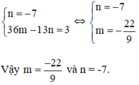

a) Ta có f(x) - 5 \(⋮\)x + 1
=> x3 + mx2 + nx + 2 - 5 \(⋮\)x + 1
=> x3 + mx2 + nx - 3 \(⋮\)x + 1
=> x = - 1 là nghiệm đa thức
Khi đó (-1)3 + m(-1)2 + n(-1) - 3 = 0
<=> m - n = 4 (1)
Tương tự ta được f(x) - 8 \(⋮\)x + 2
=> x3 + mx2 + nx - 6 \(⋮\) x + 2
=> x = -2 là nghiệm đa thức
=> (-2)3 + m(-2)2 + n(-2) - 6 = 0
<=> 2m - n = 7 (2)
Từ (1)(2) => HPT \(\left\{{}\begin{matrix}m-n=4\\2m-n=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\n=-1\end{matrix}\right.\)
Vậy đa thức đó là f(x) = x3 + 3x2 - x + 2
b) f(x) - 7 \(⋮\)x + 1
=> x3 + mx + n - 7 \(⋮\) x + 1
=> x = -1 là nghiệm đa thức
=> (-1)3 + m(-1) + n - 7 = 0
<=> -m + n = 8 (1)
Tương tự ta được : x3 + mx + n + 5 \(⋮\)x - 3
=> x = 3 là nghiệm đa thức
=> 33 + 3m + n + 5 = 0
<=> 3m + n = -32 (2)
Từ (1)(2) => HPT : \(\left\{{}\begin{matrix}3m+n=-32\\-m+n=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4m=-40\\-m+n=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-10\\n=-2\end{matrix}\right.\)
Vậy f(x) = x3 - 10x -2

http://lazi.vn/edu/exercise/biet-rang-da-thuc-px-chia-het-cho-da-thuc-x-a-khi-va-chi-khi-pa-0-hay-tim-cac-gia-tri-cua-m-va-n

Giao luu vấn đề mới
x=1, -2 là nghiệm
\(\hept{\begin{cases}a-\left(a+1\right)-\left(2b+1\right)+3b=0\\-8a-2\left(a+1\right)+2\left(2b+1\right)+3b=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}b=2\\-10a+7b=0\Rightarrow a=\frac{14}{10}=\frac{7}{5}\end{cases}}\)

Sửa đê: Q=mx^3+(m-2)x^2-(3n-5)x-4n
\(\dfrac{Q\left(x\right)}{x+1}\)
\(=\dfrac{mx^3+mx^2-2x^2-2x+\left(2-3n+5\right)x-4n}{x+1}\)
\(=mx^2-2x+\dfrac{\left(7-3n\right)x+7-3n-7-n}{x+1}\)
\(=mx^2-2x+7-3n+\dfrac{-n-7}{x+1}\)
Q(x) chia hết cho x+1
=>-n-7=0
=>n=-7
=>Q(x)=mx^3+(m-2)x^2+26x-28
\(\dfrac{Q\left(x\right)}{x-3}=\dfrac{mx^3-3mx^2+\left(4m-2\right)x^2-3\left(4m-2\right)x+\left(12m-6+26\right)x-28}{x-3}\)
\(=mx^2+\left(4m-2\right)x+\dfrac{\left(12m+20\right)x-28}{x-3}\)
\(=mx^2+\left(4m-2\right)x+\dfrac{\left(12m+20\right)x-3\left(12m+20\right)+3\left(12m+20\right)-28}{x-3}\)
\(=mx^2+\left(4m-2\right)x+12m+20+\dfrac{36m+32}{x-3}\)
Q(x) chia hết cho x-3
=>36m+32=0
=>m=-8/9

\(f\left(x\right)⋮\left(x+1\right)\)tức là chia hết cho \(\left[x-\left(-1\right)\right]\)
Do đó: \(f\left(-1\right)=0\Rightarrow n=-7\)
Tương tự, \(f\left(x\right)⋮\left(x-3\right)\)nên \(f\left(3\right)=0\)
\(\Rightarrow36m-13n-3=0\)
Giải hệ\(\hept{\begin{cases}n=-7\\36m-13n-3=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}n=-7\\m=\frac{-22}{9}\end{cases}}\)