Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho đa thức f(x)=ax5+bx3+2014x+1, biết f(2015)=2. Hãy tính f(-2015)
Giúp mk với mk cần gấp lắm!!!!!!!

Ta có : f(x)=ax5+bx3+2014x+1
=> f(2015)=a20155+b20153+2014.2015+1 và f(-2015)=a(-2015)5+b(-2015)3+2014.(-2015)+1
f(2015)+f(-2015)=a20155+b20153+2014.2015+1+a(-2015)5+b(-2015)3+2014.(-2015)+1=2
f(2015)+f(-2015)=2 mà f(2015)=2 => f(-2015)=0
Vậy......

ta có f(x)=ax5+bx3+2014x+1 \(\Rightarrow\)f(2015)=20155a+20153b+2014.2015+1 và f(-2015)=(-2015)5a+(-2015)3b+2014(-2015)+1
\(\Rightarrow\)f(2015)+f(-2015)=20155a+20153b+2014.2015+1+(-2015)5a+(-2015)3b+2014(-2015)+1=2
\(\Rightarrow\)f(2015)+f(-2015)=2 mà f(2015)=2 \(\Rightarrow\)f(-2015)=0 vậy............
NHỚ K CHO ME NHÉ !!!


\(f\left(x\right)=ax^5+bx^3+2014x+1\)
\(\Rightarrow f\left(-x\right)=a\left(-x\right)^5+b\left(-x\right)^3+2014\left(-x\right)+1\)
\(=-ax^5-bx^3-2014x+1\)
\(\Rightarrow f\left(x\right)+f\left(-x\right)=2\)
\(\Rightarrow f\left(2015\right)+f\left(-2015\right)=2\)
Mà \(f\left(2015\right)=2\Rightarrow f\left(-2015\right)=0\)

a)(x - 1) x + 2 = (x - 1)x + 4
=> (x - 1) x + 4 - (x - 1)x + 2 = 0
=> (x - 1)x + 2 . [(x - 1)2 - 1] = 0
=> \(\orbr{\begin{cases}\left(x-1\right)^{x+2}=0\\\left(x-1\right)^2-1=0\end{cases}\Rightarrow\orbr{\begin{cases}\left(x-1\right)^{x+2}=0^{x+2}\\\left(x-1\right)^2=1^2\end{cases}\Rightarrow}\orbr{\begin{cases}x-1=0\\x-1=\pm1\end{cases}}}\)
Nếu x - 1 = 0
=> x = 1
Nếu x - 1 = - 1
=> x = 0
Nếu x - 1 = 1
=> x = 2
Vậy \(x\in\left\{0;1;2\right\}\)
b) \(\left(1,78^{2x-2}-1,78^x\right):1,78^x=0\)
\(\Rightarrow1,78^{2x-2}:1,78^x-1,78^x:1,78^x=0\)
\(\Rightarrow1,78^{x-2}-1=0\)
\(\Rightarrow1,78^{x-2}=1\)
\(\Rightarrow1,78^{x-2}=1,78^0\)
\(\Rightarrow x-2=0\)
\(\Rightarrow x=2\)
Vậy x = 2

Vì : f(2015)=a20155+b20153+2014.2015+1=2
Hay: f(2015)=a20155+b20153+2014.2015=1
Nên: f(-2015)=a(-2015)5+b(-2015)3+2014.(-2015)+1
= -a20155-b20153-2014.2015+1= -(a20155+b20153+2014.2015)+1
=1-1=0
Vậy đa thức f(-2015)=0

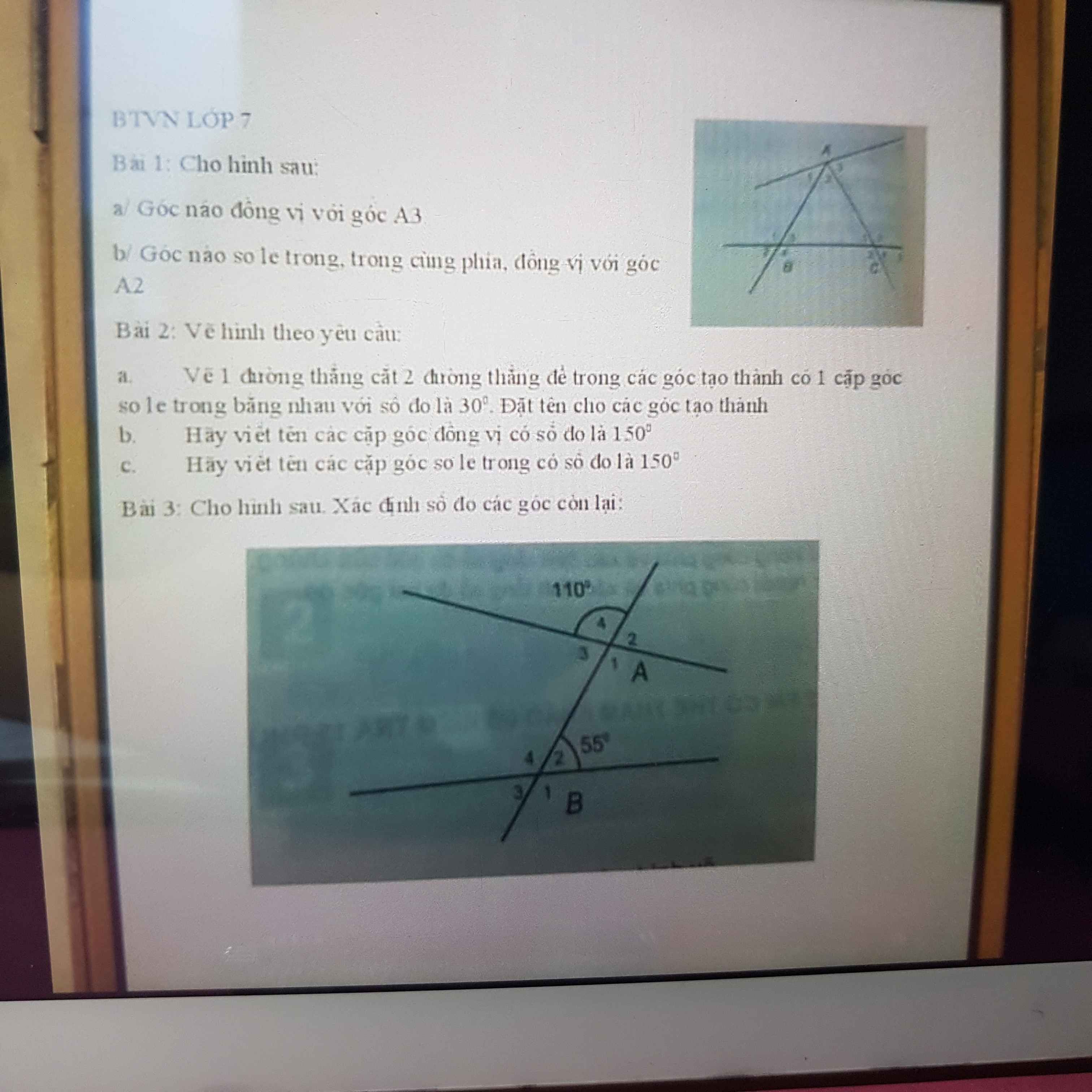
Bài 3:
\(\widehat{A_1}=110^0;\widehat{A_2}=70^0;\widehat{A_3}=70^0\)
\(\widehat{B_3}=55^0;\widehat{B_4}=125^0;\widehat{B_1}=125^0\)
f(2015)=a(2015)^5+b(2015)^3+2014.2015 +1 mà f(2015)=2 => a(2015)^5+b(2015)^3+2014.2015+1=2 =>a(2015)^5+b(2015)^3+2014.2015 =1
Xét f(-2015)=a(-2015)^5+b(-2015)^3+2014.(-2015) +1=-a(2015)^5-b(2015)^3-2014.2015 +1 = -(a(2015)^5+b(2015)^3+2014.2015)+1 =-1+1=0
bài dễ
ta có f(2015)=a.2015^5+b.2015^3+2014.2015+1
f(-2015)=a.(-2015)^5+b.(-2015)^3+2014.(-2015)+1
=>f(2015)+f(-2015)=2
(=)2+f(-2015)+2
(=) f(-2015)=0