Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(L_A=10lg\left(\frac{I_A}{I_0}\right)\Rightarrow I_A=0,1\left(Wm^2\right)\)

Khi mức cường độ âm tăng thêm 10n (dB) thì cường độ âm tăng thêm 10^n lần.
CM:
10lg(I2/I0) - 10lg(I1/I0) = 10n
=> lg(I2/I0) - lg(I1/I0) = n
=> lg(I2/I1) = n
=> I2/I1 = 10^n
=> I2 = 10^n.I1
Vậy khi mức cường độ âm nào đó tăng thêm 30dB thì cường độ của âm tăng lên 1000 lần.
Vậy B đúng
\(L=10log\frac{I}{I_0}\) Khi I tăng 1000 = 103 lần \(\Rightarrow\) L tăng 30 db
chọn B

Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)

Sử sụng hệ thức: 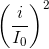 +
+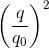 = 1
= 1
Thay số và giải hệ phương trình trìm I0 và q0
Tần số góc: ω = 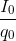 = 50 (rad/s)
= 50 (rad/s)

Do E và B biến thiên cùng pha nên, khi cảm ứng từ có độ lớn B0/2 thì điện trường E cũng có độ lớn E0/2.
Bài toán trở thành tính thời gian ngắn nhất để cường độ điện trường có độ lớn E0/2 đang tăng đến độ lớn E0/2.
E M N Eo Eo/2
Từ giản đồ véc tơ quay ta dễ dang tính được thời gian đó là t = T/3
Suy ra: \(t=\dfrac{5}{3}.10^{-7}\)s

Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)

Hướng dẫn:
\(U_{AB}=U_C=2\) (1)
\(U_{BC}^2=U_r^2+U_L^2=3\) (2)
\(U_{AC}^2=U_r^2+(U_L-U_C)^2=1\) (3)
Giải hệ 3 pt trên sẽ tìm đc \(U_r\) và \(U_L\)
Chia cho \(I\) sẽ tìm được \(r\) và \(Z_L\)
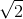
Đáp án A
+ Mức cường độ âm tại vị trí có cường độ âm I được xác định bởi biểu thức