
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

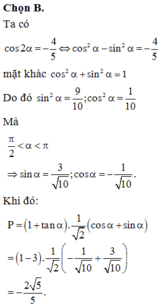

a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)

\(A=cos\left(\alpha+\dfrac{\pi}{6}\right)cos\left(\alpha-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\left[cos\left(\alpha+\dfrac{\pi}{6}+\alpha-\dfrac{\pi}{6}\right)+cos\left(\alpha+\dfrac{\pi}{6}-\alpha+\dfrac{\pi}{6}\right)\right]\)
\(=\dfrac{1}{2}\left(cos2\alpha+cos\dfrac{\pi}{3}\right)=\dfrac{1}{2}\left(\dfrac{1}{4}+\dfrac{1}{2}\right)=\dfrac{3}{8}\)

2tan a-cot a=1
=>2tana-1/tan a=1
=>\(\dfrac{2tan^2a-1}{tana}=1\)
=>2tan^2a-tana-1=0
=>(tan a-1)(2tana+1)=0
=>tan a=-1/2 hoặc tan a=1
\(P=\dfrac{tan\left(-a\right)+2\cdot cota}{3\cdot tan\left(\dfrac{pi}{2}+a\right)}=\dfrac{-tana+2\cdot cota}{-3\cdot cota}\)
TH1: tan a=-1/2
\(P=\dfrac{\dfrac{1}{2}+2\cdot\left(-2\right)}{-3\cdot\left(-2\right)}=-\dfrac{7}{2}:6=-\dfrac{7}{12}\)
TH2: tan a=1
=>cot a=1
\(P=\dfrac{-1+2}{-3}=\dfrac{1}{-3}=-\dfrac{1}{3}\)
Ta có :
\(2tan\alpha-cot\alpha=1\)
\(\Leftrightarrow2tan\alpha-\dfrac{1}{tan\alpha}=1\)
\(\Leftrightarrow2tan\alpha-\dfrac{1}{tan\alpha}-1=0\)
\(\Leftrightarrow\dfrac{2tan^2\alpha-tan\alpha-1}{tan\alpha}=0\left(tan\alpha\ne0\right)\)
\(\Leftrightarrow2tan^2\alpha-tan\alpha-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tan\alpha=1\\tan\alpha=-\dfrac{1}{2}\end{matrix}\right.\)
\(P=\dfrac{tan\left(8\pi-\alpha\right)+2cot\left(\pi+\alpha\right)}{3tan\left(\dfrac{3\pi}{2}+\alpha\right)}\)
\(\Leftrightarrow P=\dfrac{tan\left(4.2\pi-\alpha\right)+2cot\alpha}{3tan\left(2\pi-\dfrac{\pi}{2}+\alpha\right)}\)
\(\Leftrightarrow P=\dfrac{tan\left(-\alpha\right)+2cot\alpha}{3tan\left[-\left(\dfrac{\pi}{2}-\alpha\right)\right]}\)
\(\Leftrightarrow P=\dfrac{-tan\alpha+2cot\alpha}{-3tan\left(\dfrac{\pi}{2}-\alpha\right)}\)
\(\Leftrightarrow P=\dfrac{-tan\alpha+2cot\alpha}{-3cot\alpha}\)
- Với \(tan\alpha=1\Rightarrow cot\alpha=1\)
\(\Leftrightarrow P=\dfrac{-1+2.1}{-3.1}=-\dfrac{1}{3}\)
- Với \(tan\alpha=-\dfrac{1}{2}\Rightarrow cot\alpha=-2\)
\(\Leftrightarrow P=\dfrac{\dfrac{1}{2}+2.\left(-2\right)}{-3.\left(-2\right)}=\dfrac{-\dfrac{7}{2}}{6}=-\dfrac{7}{12}\)

1.a) \(4cos\dfrac{\alpha}{2}.cos\dfrac{\beta}{2}.cos\dfrac{f}{2}\)
\(=\dfrac{1}{2}.4\left[cos\left(\dfrac{\alpha-\beta}{2}\right)+cos\left(\dfrac{\alpha+\beta}{2}\right)\right].cos\dfrac{f}{2}\)
\(=2.cos\left(\dfrac{\alpha-\beta}{2}\right)cos\dfrac{f}{2}+2.cos\left(\dfrac{\alpha+\beta}{2}\right).cos\dfrac{f}{2}\)
\(=cos\left(\dfrac{\alpha-\left(\beta+f\right)}{2}\right)+cos\left(\dfrac{\alpha-\beta+f}{2}\right)+cos\left(\dfrac{\alpha+\beta-f}{2}\right)+cos\left(\dfrac{\alpha+\beta+f}{2}\right)\)
\(=cos\left(\dfrac{2\alpha-\pi}{2}\right)+cos\left(\dfrac{\pi-2\beta}{2}\right)+cos\left(\dfrac{\pi-2f}{2}\right)+cos\left(\dfrac{\pi}{2}\right)\)
\(=cos\left(-\dfrac{\pi}{2}+\alpha\right)+cos\left(\dfrac{\pi}{2}-\beta\right)+cos\left(\dfrac{\pi}{2}-f\right)\)
\(=sin\alpha+sin\beta+sinf\) (đpcm)
a2) \(1+4sin\dfrac{\alpha}{2}.sin\dfrac{\beta}{2}.sin\dfrac{f}{2}\)
\(=1+2\left[cos\left(\dfrac{\alpha-\beta}{2}\right)-cos\left(\dfrac{\alpha+\beta}{2}\right)\right].sin\dfrac{f}{2}\)
\(=1+2.cos\left(\dfrac{\alpha-\beta}{2}\right).sin\dfrac{f}{2}-2.cos\left(\dfrac{\alpha+\beta}{2}\right).sin\dfrac{f}{2}\)
\(=1+sin\left(\dfrac{f-\alpha+\beta}{2}\right)+sin\left(\dfrac{a-\beta+f}{2}\right)-sin\left(\dfrac{f-\left(\alpha+\beta\right)}{2}\right)-sin\left(\dfrac{\alpha+\beta+f}{2}\right)\)
\(=1+sin\left(\dfrac{\pi-2\alpha}{2}\right)+sin\left(\dfrac{\pi-2\beta}{2}\right)-sin\left(\dfrac{2f-\pi}{2}\right)-sin\left(\dfrac{\pi}{2}\right)\)
\(=sin\left(\dfrac{\pi}{2}-\alpha\right)+sin\left(\dfrac{\pi}{2}-\beta\right)+sin\left(\dfrac{\pi}{2}-f\right)\)
\(=cos\alpha+cos\beta+cosf\) (đpcm)

1.
\(sin\left(4x-10^0\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(4x-10^0\right)=sin45^0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-10^0=45^0+k360^0\\4x-10^0=135^0+k360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=55^0+k360^0\\4x=145^0+k360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=13,75^0+k90^0\\x=36,25^0+k90^0\end{matrix}\right.\) (\(k\in Z\))
2.
Đề không đúng
3.
ĐKXĐ: \(\left\{{}\begin{matrix}cos2x\ne0\\cosx\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(tan2x=tanx\)
\(\Rightarrow2x=x+k\pi\)
\(\Rightarrow x=k\pi\)
4.
\(cot\left(x+\dfrac{\pi}{5}\right)=-1\)
\(\Leftrightarrow x+\dfrac{\pi}{5}=-\dfrac{\pi}{4}+k\pi\)
\(\Leftrightarrow x=-\dfrac{9\pi}{20}+k\pi\) (\(k\in Z\))