Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
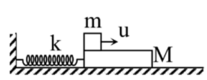
Quá trình chuyển động của vật M có thể chia thành các giai đoạn như sau:
+ Giai đoạn 1: M dao động điều hòa dưới tác dụng của lực mat sát trượt từ vị trí ban đầu A đến vị trí B.
Tần số góc của dao động ω = k M = 20 0 , 2 = 10 r a d / s
→ Biên độ dao động của vật trong giai đoạn này A 1 = F m s t k = μ m g k = 0 , 4.0 , 5.10 20 = 10 c m
+ Tốc độ của vật khi đi qua vị trí cân bằng O ′ ( F d h = F m s t ) v M = v M m a x = ω A = 100 c m / s .
Ta để ý rằng u = 0 , 5 v m a x → tại vị trí x = 3 2 A 1 thì v M = u → không còn chuyển động tương đối giữa hai vật → ma sát lúc này là ma sát nghỉ.
+ Giai đoạn 2: Hai vật M + m dính chặt vào nhau dao động điều hòa quanh vị trí lò xo không biến dạng.
Tần số góc của dao động trong giai đoạn này ω ' = k M + m = 20 0 , 2 + 0 , 5 = 5 , 3
→ Biên độ dao động của vật trong giai đoạn này: A 2 = A 1 − 3 2 A 1 2 + u ω ' 2 = 10 − 5 3 2 + 50 5 , 3 2 = 9 , 5 c m
+ Rõ ràng biên độ A 2 = A m a x = μ g ω ' 2 = 0 , 4.10 5 , 3 2 ≈ 14 cm, nên trong giai đoạn trên không có sự trượt lên nhau giữa M và m.
→ Tổng quãng đường vật đi được là S = A 2 = 9 , 5 c m .
Vận tốc của hai vật sau va chạm: (M + m)V = mv
=> V = 0,02\(\sqrt{2}\) (m/s)
Tọa độ ban đầu của hệ hai vật x0 = \(\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2+\left(M+m\right)}{k}=0,0016\Rightarrow A=0,04m=4cm\)
→ B
Vận tốc của hai vật sau va chạm: \(\left(M+m\right)V=mv\)
\(\rightarrow V=0,02\sqrt{2}\left(m\text{ /}s\right)\)
Tọa độ ban đầu của hệ hai vật: \(x_0=\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}=0,04m=4cm\)
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2\left(M+m\right)}{k}=0,0016\) \(\rightarrow A=0,04m=4cm\)
Đáp án B
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)
Sau mỗi nửa chu kì, biên độ của con lắc giảm là:
\(2\dfrac{\mu.mg}{k}=2\dfrac{0,01.0,1.10}{100}=0,0001m=0,1mm.\)
Sau mỗi lần vật qua VTCB thì đúng bằng nửa chu kì, do đó biên độ dao động giảm là 0,1 mm.
Khi vật I qua VTCB thì nó có vận tốc là: \(v=\omega.A\)
Khi thả nhẹ vật II lên trên vật I thì động lượng được bảo toàn
\(\Rightarrow M.v = (M+m)v'\Rightarrow v'=\dfrac{3}{4}v\)
Mà \(v'=\omega'.A'\)
\(\dfrac{v'}{v}=\dfrac{\omega'}{\omega}.\dfrac{A'}{A}=\sqrt{\dfrac{M}{\dfrac{4}{3}M}}.\dfrac{A'}{A}=\dfrac{3}{4}\)
\(\Rightarrow \dfrac{A'}{A}=\dfrac{\sqrt 3}{2}\)
\(\Rightarrow A'=5\sqrt 3cm\)
Chọn A.
Vận tốc của M khi qua VTCB: v = ωA = 10.5 = 50cm/s
Vận tốc của hai vật sau khi m dính vào M: v’ = Mv/(M+v)= 40cm/s
Cơ năng của hệ khi m dính vào M: W = 1/2KA'2= 1/2(m+M)v'2
A’ = 2căn5
nói lại em kém anh 7 năm nhé. Nên bọn em cần gợi ý mới làm được chứ. Với lại hình như anh học cái này thì phải bít chứ. Its ra cũng phải có gợi ý...!
Hướng dẫn: Chọn đáp án A
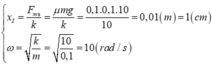
Lần 1 qua I thì I là tâm dao động với biên độ so với I:
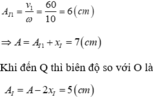
Tiếp theo thì I’ là tâm dao động và biên độ so với I’ là
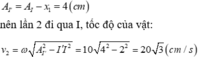
Tiếp đến vật dừng lại ở điểm cách O một khoảng
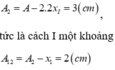
và lúc này I là tâm dao động nên lần thứ 3 đi qua I nó có tốc độ:
Chú ý: Giả sử lúc đầu vật ở O ta truyền cho nó một vận tốc để đến được tối đa là điểm . Độ giảm cơ năng đúng bằng công của lực ma sát
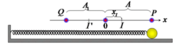
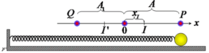
Đán áp A
Quá trình chuyển động của vật M có thể chia thành các giai đoạn như sau:
Giai đoạn thứ nhất: khi vật m trượt trên vật M, lực mà sát trượt luông không đổi, ta có thể xem chuyển động của M như dao động của vật vật chịu tác dụng của lực không đổi.
Khi đó vật M sẽ tiến về vị trí cân bằng O, với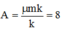
cm và tốc độ cực đại có thể đạt được khi đến O là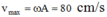 
+ Giai đoạn thứ hai: trong quá trình dao động đến vị trí cân bằng O, M đi qua A, lúc này vận tốc của M tăng lên đúng bằng u = 50 cm/s, chuyển động tương đối giữa M và m là không còn, lực ma sát giữa chúng là lực ma sát nghỉ. Hai vật dính chặt vào nhau chuyển động với cùng vận tốc u = 50 cm/s.
+ Giai đoạn thứ 3: Hệ hai vật cùng chuyển động với vận tốc 50 cm/s đến O, lúc này lực đàn hồi lớn hơn lực ma sát nghỉ, vật M chậm dần và có sự chuyển động tương đối giữa M và m, bây giờ vật M được xem là dao động điều hòa dưới tác dụng của ngoại lực không đổi như giai đoạn thứ nhất. Vật M sẽ dừng lại tại biên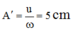
Vậy tổng quãng đường M đi được là 8 + 5 = 13 cm.