Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x + 2 P x - 2 = x - 1 Q x 2 - 4
⇒ x + 2 . P . x 2 - 4 = x - 2 x - 1 . Q
Hay (x + 2)(x – 2)(x + 2).P = (x – 2)(x – 1).Q
Chọn P = (x – 1) thì Q = x + 2 2

Ta có:
(...) . (x-4) = x . ( x2- 16 )
= x(x - 4)(x + 4) = (x2 + 4x)(x -4)
Vậy phải điền vào chỗ trống đa thức x(x + 4) hay x2 + 4x.
Ta có: (…)(x – 4) = x(x2 – 16) = x(x - 4)(x + 4) = (x2 + 4x)(x -4)
Vậy phải điền vào chỗ trống đa thức x(x + 4) hay x2 + 4x.

\(1.x^2-4x+4=8\left(x-2\right)^5\)
\(\Leftrightarrow\left(x-2\right)^2-8\left(x-2\right)^5=0\)
\(\Leftrightarrow\left(x-2\right)^2\left[1-8\left(x-2\right)^3\right]=0\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x-2\right)^2=0\\1-8\left(x-2\right)^3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\\left(x-2\right)^3=\frac{1}{8}\end{cases}\Rightarrow\orbr{\begin{cases}x=2\\x=\frac{5}{2}\end{cases}}}\)
\(T=4\left(a^3+b^3\right)-6\left(a^2+b^2\right)\)
\(=4\left(a+b\right)\left(a^2-ab+b^2\right)-6a^2-6b^2\)
\(=4\left(a^2-ab+b^2\right)-6a^2-6b^2\)(Vì a+b=1)
\(=4a^2-4ab+3b^2-6a^2-6b^2\)
\(=-2a^2-4ab-2b^2\)
\(=-2\left(a+b\right)^2=-2\)

a) \(\dfrac{\left(x+2\right)P}{x-2}=\dfrac{\left(x-1\right)Q}{x^2-4}\)
\(\Leftrightarrow\left(x^2-4\right)\left(x+2\right)P=\left(x-2\right)\left(x-1\right)Q\)
\(\Leftrightarrow\)\(\left(x+2\right)^2\left(x-2\right)P=\left(x-2\right)\left(x-1\right)Q\)
\(\Leftrightarrow\)\(\left(x+2\right)^2P=\left(x-1\right)Q\)
\(\Leftrightarrow P=x-1\)
\(Q=\left(x+2\right)^2=x^2+4x+4\)
b)\(\dfrac{\left(x+2\right)P}{x^2-1}=\dfrac{\left(x-2\right)Q}{x^2-2x+1}\)
\(\Leftrightarrow\left(x-1\right)^2\left(x+2\right)P=\left(x+1\right)\left(x-1\right)\left(x-2\right)Q\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)P=\left(x+1\right)\left(x-2\right)Q\)
\(\Leftrightarrow P=\left(x+1\right)\left(x-2\right)=x^2-x-2\)
\(Q=\left(x-1\right)\left(x+2\right)=x^2+x-2\)

\(\begin{array}{l}\frac{{2{{\rm{x}}^2} + 1}}{{4{\rm{x}} - 1}} = \frac{{8{{\rm{x}}^3} + 4{\rm{x}}}}{Q}\\ \Rightarrow Q = \frac{{\left( {8{{\rm{x}}^3} + 4{\rm{x}}} \right)\left( {4{\rm{x}} - 1} \right)}}{{2{{\rm{x}}^2} + 1}}\\Q = \frac{{4{\rm{x}}\left( {2{{\rm{x}}^2} + 1} \right)\left( {4{\rm{x}} - 1} \right)}}{{2{{\rm{x}}^2} + 1}}\\Q = 4{\rm{x}}\left( {4{\rm{x}} - 1} \right) = 16{{\rm{x}}^2} - 4{\rm{x}}\end{array}\)
Đáp án D
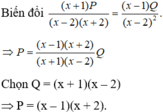
có thể giải thích rõ hơn bước 2 tại sao ra như vậy ko bn