
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) ΔADB và ΔABC vuông có ∠B chung ∠ ΔADB ∼ ΔCAB (g.g)
b) Vì ∠B = 2∠C (gt) ∠ ∠B1 = ∠B2 = ∠C
Do đó hai tam giác vuông ABE và ACB đồng dạng (g.g)
![]()
c) Ta có ΔADB ∼ ΔCAB (cmt)
![]()
Theo tính chất đường phân giác ta có :

d) Ta có AB = 2BD (gt)
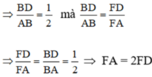
![]()


bài 1
E là TĐ của BC , F là TĐ của AC nên EF là đường trung bình của tam giác ABC➡ EF//AB (1) , EF=½AB (2)
Tứ giác AEFB có góc A =90 độ , EF//AB➡ AEFB là hình thang vuông
b) SABC = (AB✖ AC)/2➡ AB= (2✖ SABC)/AC =12cm
thay AB =12 vào (2)➡ EF=6cm
E là TĐ của AC➡ AE=8cm
vì EF//AB , AB vuông góc vs AC nên EF vuông góc vs AC hay góc AEF =90 độ
xét tam giác AEF vuông tại E , áp dụng định lí pytago tìm đượcAF=10cm
AF và BE cắt nhau tại I ➡ I là trọng tâm của tam giác ABC ➡ CN là trung tuyến ➡ N là TĐ của AB
b)EF=½AB , NA=½AB➡ EF=NA(3)
EF//AB➡ EF//NA(4)
từ (3) và (4)➡ AEFN là HBH
HBH AEFN có góc A =90độ ➡ AEFN là HCN
c)E là TĐ của AC , N là TĐ của BA➡ EF là đường trung bình của tam giác ABC ➡ EN//FC , EN=FC ➡ CENF là HBH

Ta có: a < b ⇒ a + c < b + c (1)
c < d ⇒ b + c < b + d (2)
Từ (1) và (2) suy ra: a + c < b + d.

Bài 1 bạn viết rõ yêu cầu của đề ra nhé , mình làm bài 2.
\(a.\left(a-b\right)^2=2\left(a^2+b^2\right)\)
\(\Leftrightarrow2a^2+2b^2-a^2+2ab-b^2=0\)
\(\Leftrightarrow\left(a+b\right)^2=0\)
\(\Leftrightarrow a+b=0\)
\(\Leftrightarrow a=-b\left(đpcm\right)\)
\(b.a^2+b^2+c^2=ab+bc+ac\)
\(\Leftrightarrow2a^2+2b^2+2c^2=2ab+2bc+2ac\)
\(\Leftrightarrow a^2-2ab+b^2+b^2-2bc+c^2+a^2-2ac+c^2=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=b\\b=c\\c=a\end{matrix}\right.\)\(\Leftrightarrow a=b=c\left(đpcm\right)\)
\(c.\left(a+b+c\right)^2=3\left(ab+bc+ac\right)\)
\(\Leftrightarrow a^2+b^2+c^2=3ab+3bc+3ac-2ab-2bc-2ac\)
\(\Leftrightarrow a^2+b^2+c^2=ab+bc+ac\)
\(\Leftrightarrow a=b=c\) ( Kết quả câu b)

a<b; c<d
=>a+c(hai số nhỏ hơn)<b+d(hai số lớn hơn)
có vậy thôi
vìtổng của hai số nhỏ hơn vẫn chỉ nhỏ hơn tổng hai số lớn