Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

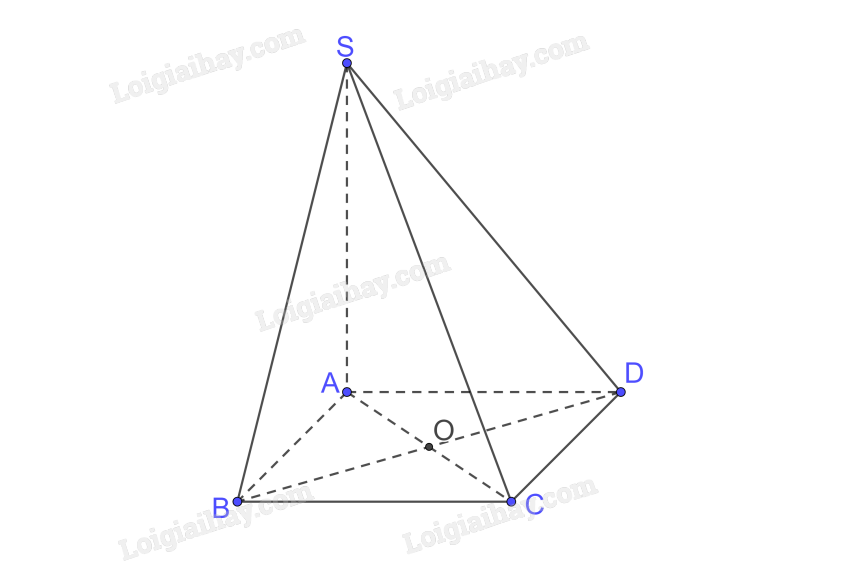
a) A là hình chiếu của S trên (ABCD) \(\left( {SA \bot \left( {ABCD} \right)} \right)\)
C là hình chiếu của C trên (ABCD)
\( \Rightarrow \) AC là hình chiếu của SC trên (ABCD)
\( \Rightarrow \) \(\left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
Xét tam giác ABC vuông tại B có
\(A{C^2} = A{B^2} + B{C^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \)
Xét tam giác SAC vuông tại A có
\(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{a\sqrt 2 }}{{a\sqrt 2 }} = 1 \Rightarrow \widehat {SCA} = {45^0}\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = {45^0}\)
b) \(\left. \begin{array}{l}AC \bot BD\left( {hv\,\,ABCD} \right)\\SA \bot BD\left( {SA \bot \left( {ABCD} \right)} \right)\\AC \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow \left( {BD,\left( {SAC} \right)} \right) = {90^0}\)
c) Gọi \(AC \cap BD = \left\{ O \right\}\) mà \(BD \bot \left( {SAC} \right)\)
\( \Rightarrow \) O là hình chiếu của B trên (SAC)
S là hình chiếu của S trên (SAC)
\( \Rightarrow \) SO là hình chiếu của SB trên (SAC).

Đáp án C
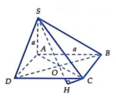
Gọi H là hình chiếu của C trên SO(O = AC ∩ BD), vì góc SOC tù nên H nằm ngoài SO
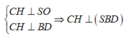
=> Góc tạo bởi SC và (SBD) là C S O ^
Ta có ![]()
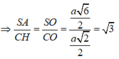
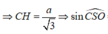
![]()

Đáp án A.
Gọi H là hình chiếu của C trên SO và góc S O C ^ tù nên H nằm ngoài đoạn SO => CH ⊥ (SBD)
=> Góc tạo bởi SC và (SBD) là C S O ^
Lại có ![]()
![]()
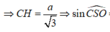
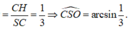

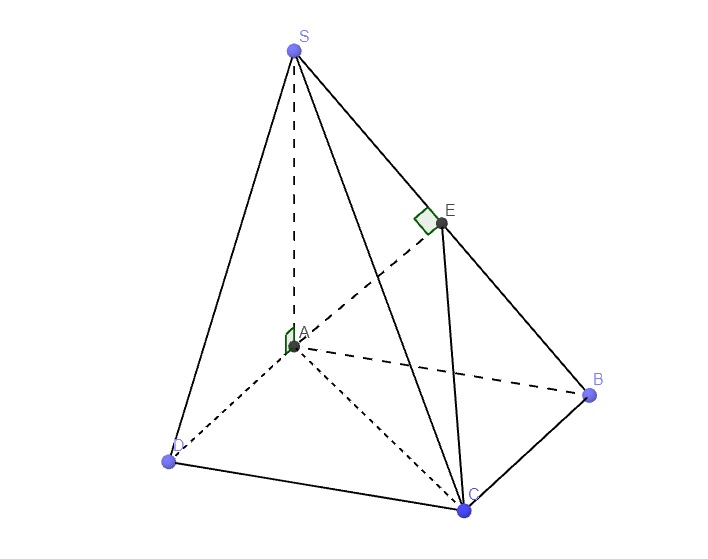
Từ A kẻ \(AE\perp SB\) (\(E\in SB\))
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp AE\)
\(\Rightarrow AE\perp\left(SBC\right)\)
\(\Rightarrow\widehat{ACE}\) là góc giữa AC và (SBC)
Hệ thức lượng trong tam giác SAB:
\(\dfrac{1}{AE^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\Rightarrow AE=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a\sqrt{3}}{2}\)
\(AC=AB\sqrt{2}=a\sqrt{2}\)
\(\Rightarrow sin\widehat{ACE}=\dfrac{AE}{AC}=\dfrac{\sqrt{6}}{4}\)

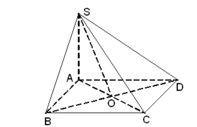
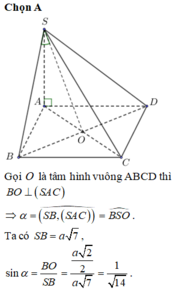
Gọi O là tâm của hình vuông ABCD.
● Ta có:
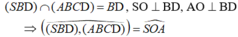
● ΔSAO vuông tại A