Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chứng minh được MN//PQ (cùng vuông góc với AC). Chứng minh được MP = QN. Þ ĐPCM.
b) Ta có:
S M N E = 1 2 S M E N C , S N P E = 1 2 S P B N E , S P Q E = 1 2 S , A P E Q S M Q E = 1 2 S Q E M D ⇒ S M N P Q = 1 2 S A B C S .
c) Chu vi MNPQ = MN + PQ + NP + QM
= EC + AE + BE + ED = AC + BE + ED.
Trong tam giác BED, BE + ED ³ BD
Þ Chu vi MNPQ ≥ AC + BD
Þ E là tâm của hình vuông ABCD

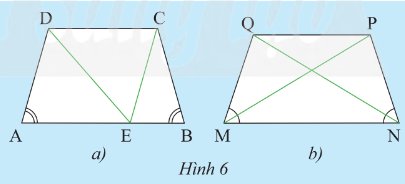
a) i) \(ABCD\) là hình thang cân (gt)
\( \Rightarrow \widehat A = \widehat B\) (1) và \(DC\) // \(AE\)
Vì \(AD\;{\rm{//}}\;CE\) (gt)
\(\widehat A = \widehat {CEB}\) (cặp góc đồng vị) (2)
Từ (1) và (2) suy ra: \(\widehat {CEB} = \widehat B\)
Suy ra \(\Delta CEB\) là tam giác cân.
ii) \(\Delta CEB\) cân tại \(C\) (cmt)
Suy ra: \(CE = BC\) (3)
Xét \(\Delta ADE\) và \(\Delta CED\) ta có:
\(\widehat {{\rm{ADE}}} = \widehat {{\rm{CED}}}\) (\(AD\)// \(CE\), cặp góc so le trong)
\(DE\) chung
\(\widehat {{\rm{AED}}} = \widehat {{\rm{CDE}}}\) (\(CD\) // \(AB\), cặp góc so le trong)
Suy ra: \(\Delta ADE = \Delta CED\) (g-c-g)
Suy ra: \(AD = CE\) (4)
Từ (3) và (4) suy ra: \(AD = BC\)
b) Chứng minh tương tự như ý a) ta có: Hình thang cân \(MNPQ\) có hai cạnh bên \(MQ = NP\)
Xét tam giác \(\Delta MQP\) và \(\Delta NPQ\) ta có:
\(MQ = NP\) (cmt)
\(\widehat {{\rm{MQP}}} = \widehat {{\rm{NPQ}}}\) (do \(MNPQ\) là hình thang cân)
\(PQ\) chung
Suy ra: \(\Delta MQP = \Delta NPQ\) (c-g-c)
\( \Rightarrow MP = NQ\) (hai cạnh tương ứng)