Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

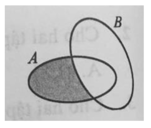
Phần tô đậm thuộc A nhưng không thuộc A ∩ B .
Phần tô đậm là tập con của A nên phần tô đậm thuộc C A ( A ∩ B )
Đáp án D

Bài 4: B
Bài 5:
a: {3;5};{3;7};{5;7};{3;5;7};{3};{5};{7};\(\varnothing\)

Đáp án: B
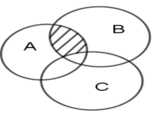
Phần bị gạch là phần thuộc (A ∩ B) nhưng không thuộc C nên phần bị gạch biểu thị cho (A ∩ B) \ C.

Ta có:
Tập hợp A:
\(A=\left\{1;2;5\right\}\)
Tập hợp B:
\(B=\left\{1;3;4;5\right\}\)
Tập hợp \(A\cap B\) là:
\(\left\{1;5\right\}\)
⇒ Chọn D

Đáp án: D
Nhìn vào hình vẽ ta thấy vùng 1 là tập hợp các phần tử thuộc A mà không thuộc B nên vùng 1 là A \ B;
Vùng 2 là tập hợp các phần tử vừa thuộc A vừa thuộc B nên vùng 2 là A ∩ B; Vùng 3 là tập hợp các phần tử thuộc B mà không thuộc A nên vùng 3 là B \ A; Vùng 4 là tập hợp các phần tử thuộc E mà không thuộc A; B nên vùng 4 là E \ (A ∪ B).
Vậy cả 4 phát biểu đều đúng

a: A=[1;+∞)
B=(-∞;3]
b: A giao B=[1;3]
A hợp B=R
A\B=(3;+∞)
B\A=(-∞;1)

a) \(A = \{ x \in \mathbb{N}|\;x < 2\} = \{ 0;1\} \) và \(B = \{ x \in \mathbb{R}|\;{x^2} - x = 0\} = \{ 0;1\} \)
Vậy A = B, A là tập con của tập B và ngược lại.
b) D là tập hợp con của C vì: Mỗi hình vuông đều là một hình thoi đặc biệt: hình thoi có một góc vuông.
\(C \ne D\) vì có nhiều hình thoi không là hình vuông, chẳng hạn:
c) \(E = ( - 1;1] = \left\{ {x \in \mathbb{R}|\; - 1 < x \le 1} \right\}\) và \(F = ( - \infty ;2] = \left\{ {x \in \mathbb{R}|\;x \le 2} \right\}\)
E là tập con của F vì \( - 1 < x \le 1 \Rightarrow x \le 2\) .
\(E \ne F\) vì \( - 3 \in F\)nhưng \( - 3 \notin E\)
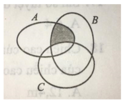
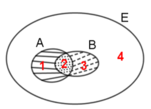
Ta thấy miền tô đậm thuộc tập A ∩ B nhưng không thuộc tập hợp C.
Do đó, miền tô đậm biểu diễn tập hợp ( A ∩ B ) \ C
Đáp án B