I
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
13 tháng 4 2021
Lời giải:
Bạn nhớ tới bổ đề sau: Với $a,b>0$ thì $a^3+b^3\geq ab(a+b)$.
Áp dụng vào bài:
$5a^3-b^3\leq 5a^3-[ab(a+b)-a^3]=6a^3-ab(a+b)$
$\Rightarrow \frac{5a^3-b^3}{ab+3a^2}\leq \frac{6a^3-ab(a+b)}{ab+3a^2}=\frac{6a^2-ab-b^2}{3a+b}=\frac{(3a+b)(2a-b)}{3a+b}=2a-b$
Tương tự:
$\frac{5b^3-c^3}{bc+3b^2}\leq 2b-c; \frac{5c^3-a^3}{ca+3c^2}\leq 2c-a$
Cộng theo vế:
$\Rightarrow \text{VT}\leq a+b+c=3$
Ta có đpcm
Dấu "=" xảy ra khi $a=b=c=1$
22 tháng 8 2017
Ta có : \(\frac{1}{a^2+b^2+c^2}+\frac{2009}{ab+bc+ca}\)
\(=\frac{1}{a^2+b^2+c^2}+\frac{1}{ab+bc+ca}+\frac{1}{ab+bc+ca}+\frac{2007}{ab+bc+ca}\)
Áp dụng bđt Cauchy Schwaz dạng Engel ta có :
\(\frac{1}{a^2+b^2+c^2}++\frac{1}{ab+bc+ca}+\frac{1}{ab+bc+ca}\ge\frac{\left(1+1+1\right)^2}{a^2+b^2+c^2+2ab+2bc+2ac}\)
\(=\frac{9}{\left(a+b+c\right)^2}\le\frac{9}{3^2}=1\)(1)
Ta lại có : \(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac\ge0\)
\(\Leftrightarrow a^2+b^2+c^2\ge ab+ac+bc\)
\(\Leftrightarrow\left(a^2+b^2+c^2+2ab+2bc+2ac\right)\ge3ab+3bc+3ac\)
\(\Leftrightarrow\left(a+b+c\right)^2\ge3\left(ab+ac+bc\right)\Leftrightarrow9\ge3\left(ab+ac+bc\right)\)
\(\Rightarrow ab+ac+bc\le3\Rightarrow\frac{2007}{ab+ac+bc}\ge\frac{2007}{3}=669\)(2)
Cộng vế với vế của (1) và (2) ta được :
\(\frac{1}{a^2+b^2+c^2}+\frac{1}{ab+bc+ac}+\frac{1}{ab+ac+bc}+\frac{2007}{ab+ac+bc}\ge669+1=670\)
Hay \(\frac{1}{a^2+b^2+c^2}+\frac{2009}{ab+bc+ac}\ge670\)(đpcm) (Dấu "=" xảy ra <=> a = b = c = 1)
NP
1
12 tháng 10 2017
Câu hỏi của Lê Văn Hoàng - Toán lớp 9 - Học toán với OnlineMath
17 tháng 1 2022
Áp dụng bất đẳng thức Chevbyshev cho hai bộ đơn điệu cùng chiều \(\left(\dfrac{2}{a+b},\dfrac{2}{b+c},\dfrac{2}{c+a}\right)\) và \(\left(c\left(a+b\right),a\left(b+c\right),b\left(c+a\right)\right)\) ta có \(2c+2a+2b=\dfrac{2}{a+b}.c\left(a+b\right)+\dfrac{2}{b+c}.a\left(b+c\right)+\dfrac{2}{c+a}.b\left(c+a\right)\ge\dfrac{1}{3}\left(\dfrac{2}{a+b}+\dfrac{2}{b+c}+\dfrac{2}{c+a}\right)\left(a\left(b+c\right)+b\left(c+a\right)+c\left(a+b\right)\right)=\dfrac{2}{3}\left(ab+bc+ca\right)\left(\dfrac{2}{a+b}+\dfrac{2}{b+c}+\dfrac{2}{c+a}\right)\).
Mà \(\dfrac{2}{a+b}+\dfrac{2}{b+c}+\dfrac{2}{c+a}=a+b+c\) nên \(ab+bc+ca\le3\).
6 tháng 5 2021
Ta có \(\sqrt{1+a^2}+\sqrt{2a}\le\sqrt{2\left(1+a^2+2a\right)}=\sqrt{2}\left(a+1\right)\).
Tương tự \(\sqrt{1+b^2}+\sqrt{2b}\le\sqrt{2}\left(b+1\right)\); \(\sqrt{1+c^2}+\sqrt{2c}\le\sqrt{2}\left(c+1\right)\).
Lại có \(\left(2-\sqrt{2}\right)\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)\le\left(2-\sqrt{2}\right)\sqrt{3\left(a+b+c\right)}\le3\left(2-\sqrt{2}\right)\).
Do đó \(B\le\sqrt{2}\left(a+b+c+3\right)+3\left(2-\sqrt{2}\right)\le6\sqrt{2}+6-3\sqrt{2}=3\sqrt{2}+6\).
Dấu "=" xảy ra khi a = b = c = 1.
DN
0
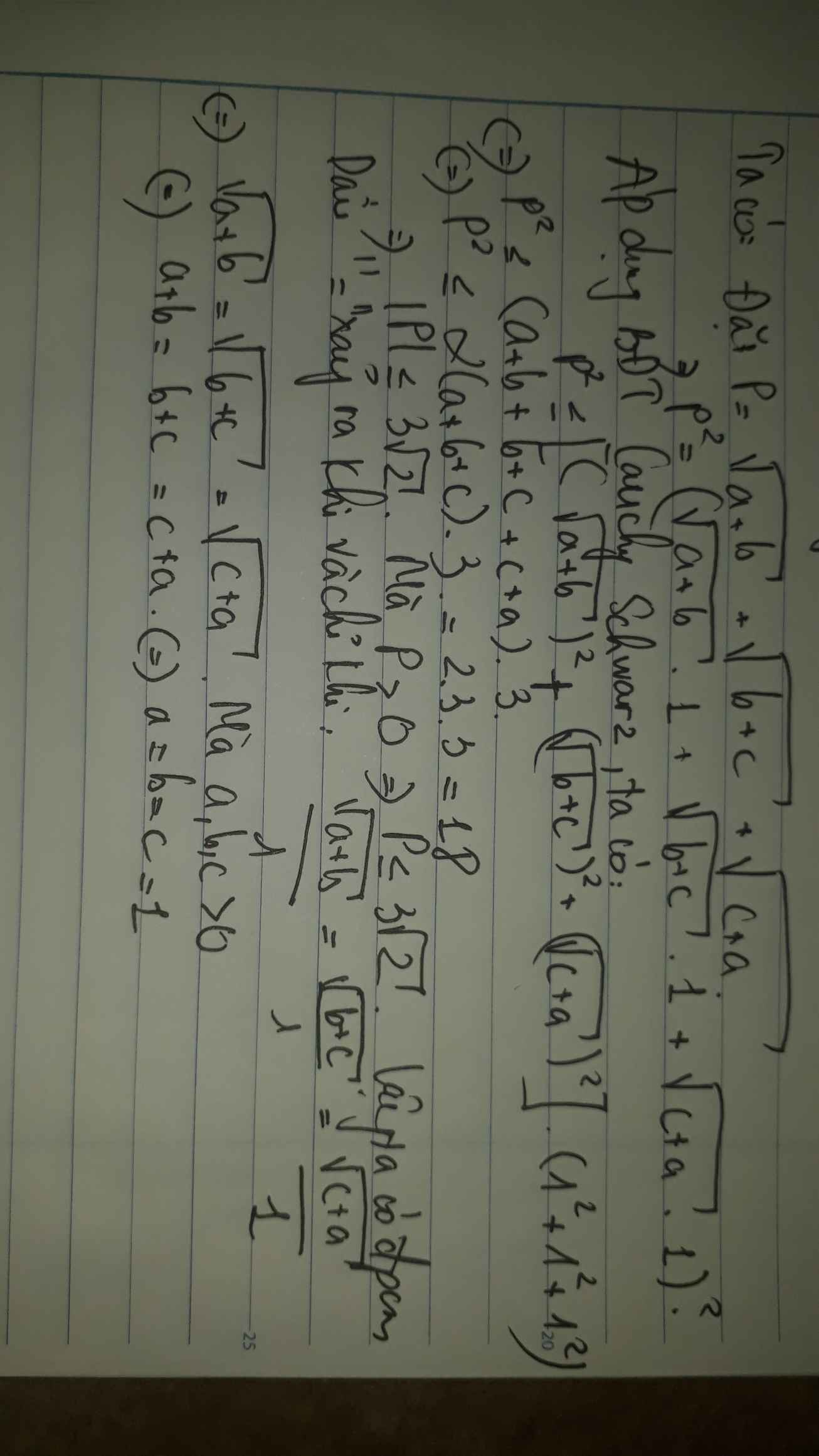
đề chiều nay e thi đấy
thoi nghỉ ik e :))