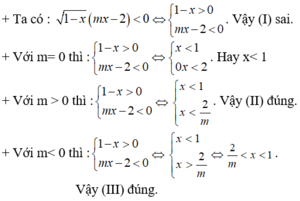Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: Xét ΔOHA vuông tại A và ΔOHB vuông tại B có
OH chung
\(\widehat{AOH}=\widehat{BOH}\)
Do đó: ΔOHA=ΔOHB
Suy ra: HA=HB
hay ΔHAB cân tại H
b: Xét ΔOAB có
OH là đường cao
AD là đường cao
OH cắt AD tại C
Do đó: C là trực tâm của ΔOAB
Suy ra: BC\(\perp\)Ox
c: \(\widehat{HOA}=\dfrac{60^0}{2}=30^0\)
Xét ΔOHA vuông tại A có
\(\cos HOA=\dfrac{OA}{OH}\)
\(\Leftrightarrow OA=\dfrac{\sqrt{3}}{2}\cdot4=2\sqrt{3}\left(cm\right)\)

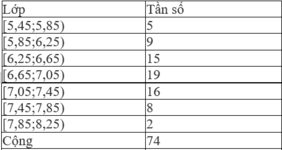
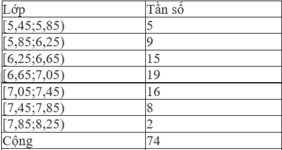
Công thức số trung bình
x = 6 , 65 . 5 + 6 , 05 . 9 + 6 , 45 . 15 + 6 , 85 . 19 + 7 , 25 . 16 + 7 , 65 . 8 + 8 , 05 . 2 74 ≈ 6 , 8
Công thức độ lệch chuẩn
s 2 = 5 , 65 - 6 , 8 2 . 5 + 6 , 05 - 6 , 8 2 . 9 + 6 , 45 - 6 , 8 2 . 15 74 + 6 , 85 - 6 , 8 2 . 19 + 7 , 25 - 6 , 8 2 . 8 + 8 , 05 - 6 , 8 2 . 2 74 = 0 , 3473
Suy ra s ≈ 0 , 589
b) Đáp án là A.

Hàm số y = m - 2 x - x + 1 xác định khi và chỉ khi m - 2 x ≥ 0 x + 1 ≥ 0 ⇔ x ≤ m 2 x ≥ - 1 .
Do đó tập xác định của hàm số y = m - 2 x - x + 1 là một đoạn trên trục số khi và chỉ khi m 2 > - 1 ⇔ m > - 2

Ta bổ sung thêm một cột ghi giá trị đại diện của mỗi lớp:
Lớp |
Tần số |
Giá trị đại diện |
| [5,45;5,85) | 5 |
5,65 |
[5,85;6,25) |
9 |
6,05 |
[6,25;6,65) |
15 |
6,45 |
[6,65;7,05) |
19 |
6,85 |
[7,05;7,45) |
16 |
7,25 |
[7,45;7,85) |
8 |
7,65 |
[7,85;8,25) |
2 |
8,05 |
Cộng |
74 |
|
Áp dụng công thức ta tìm được số trung bình :
x = 5 , 65 . 5 + 6 , 05 . 9 + 6 , 45 . 15 + 6 , 85 . 19 + 7 , 25 . 16 + 7 , 65 . 8 + 8 , 05 . 2 74 ≈ 6 , 8
Đáp án là D.

a/b=2/7
=>b=7/2a
b/c=14/15
=>b=14/15c
=>7/2a=14/15c
=>a=4/15c
Vậy: a:c=4/15

b: Tọa độ điểm A là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}-x+1=x+1\\y=x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
Tọa độ điểm B là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}y=-1\\-x+1=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=2\end{matrix}\right.\)
Tọa độ điểm C là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}y=-1\\x+1=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-1\end{matrix}\right.\)

Ta có; x < A ⇔ - A < x < A .
Suy ra; nếu a < b thì - b < a < b ⇒ - b ≤ a ≤ b

Nếu a, b là những số thực và a ≤ b thì a 2 ≤ b 2 ⇔ a 2 ≤ b 2