Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: G là trực tâm tam giác MNP
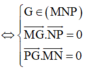
Cách giải: Gọi G x 0 ; y 0 ; z 0 là trực tâm tam giác MNP
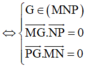
![]()
Mặt phẳng (MNP) có một VTPT
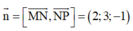
Phương trình (MNP) 2x+3y-z-4=0
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Từ (1),(2),(3), suy ra
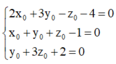
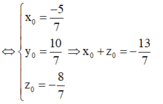

Chọn C
Gọi G là trọng tâm tam giác ABC => G = (2; 1; 3)
Khi đó ![]()
Nên ![]() có giá trị nhỏ nhất khi và chỉ khi MG ngắn nhất, khi đó M là hình chiếu vuông góc của G (2; 1; 3) trên (Oxy)
có giá trị nhỏ nhất khi và chỉ khi MG ngắn nhất, khi đó M là hình chiếu vuông góc của G (2; 1; 3) trên (Oxy)
Do đó M (2; 1; 0).
Vậy ![]()

Đáp án C
Gọi G là trọng tâm của tam giác ABC => G(2;1;3)

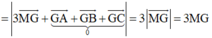
Suy ra MG min <=>M là hình chiếu của G trên (Oxy) => M(2;1;0)

Đáp án D
Phương trình mặt phẳng trung trực của AB là
![]()
Phương trình mặt phẳng trung trực của AC là
![]()
Chọn x = 1
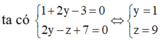
![]()
Phương trình đường thẳng giao tuyến của ( α ) và ( β ) là
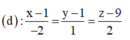
Vì MA=MB=MC
![]()
![]()
![]()
![]()
![]()

Chọn A
Do a → , b → cùng phương và nên b → =k a → (k ≠ 0) ta có
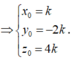
Suy ra
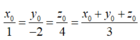
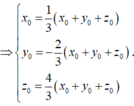
Theo giả thiết vectơ b → tạo với tia Oy một góc nhọn nên
![]()
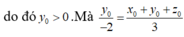
![]()
![]()
suy ra
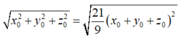
![]()
![]()
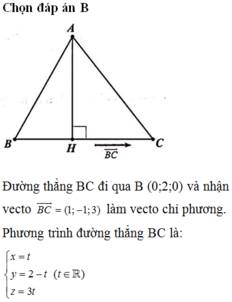


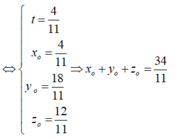


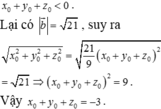
Đáp án A