Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Ta có: 2 y = x + 3 ⇒ y = 1 2 x + 3 2 . Với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng y nên 2y = x+3 là một hàm số
+ Ta có: − y = x 2 ⇒ y = − x 2 . Với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y nên là một hàm số
+ Ta có: y = x 2 + 3 là một hàm số vì với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y
Đáp án cần chọn là D

Nhận thấy y - 3 = x ⇒ y = x + 3 là một hàm số
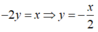 là một hàm số
là một hàm số
Với y 2 = x ta thấy khi x = 4 thì y 2 = 4 suy ra y = 2 hoặc y = -2 nên với một giá trị của x cho hai giá trị của y nên y không là hàm số của x
Chọn đáp án C

Nhận thấy y - 3 = x ⇒ y = x + 3 là một hàm số
-2y = x ⇒ y = -x/2 là một hàm số
Với y2 = x ta thấy khi x = 4 thì y2 = 4 suy ra y = 2 hoặc y = -2 nên với một giá trị của x cho hai giá trị của y nên y không là hàm số của x
Chọn đáp án C

Nhận thấy y − 3 = x ⇒ y = x + 3 là một hàm số
− 2 y = x ⇒ y = − x 2 là một hàm số
Với y 2 = x ta thấy khi x = 4 thì y 2 = 4 suy ra y = 2 hoặc y = -2 nên với một giá trị của x cho hai giá trị của y nên y không là hàm số của x
Đáp án cần chọn là C

- Công thức biểu diễn diện tích y theo x là y = 3x
- Vì với mỗi giá trị của x ta xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số đại lượng x
- Vẽ đồ thị hàm số :
+ Chọn 1 điểm khác O thuộc đồ thị : chọn x = 1 được y = 3 ⇒ A(1 ;3) thuộc đồ thị.
+ Đường thằng OA là đồ thị hàm số y = 3x
Vẽ đồ thị:
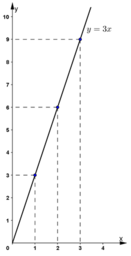
Trên đồ thị thấy :
+ Điềm thuộc đồ thị có x = 3 thì ứng với y = 9
Vậy khi x = 3 m thì diện tích hình chữ nhật bằng 9(m2)
+ Điểm thuộc đồ thị có x = 4 thì ứng với y = 12
Vậy khi x = 4 m thì diện tích hình chữ nhật bằng 12 (m2)

Điểm thuộc đồ thị có y = 6 thì ứng với x = 2 .
Vậy khi diện tích hình chữ nhật bằng 6(m2) thì cạnh x = 2 (m)
Điểm thuộc đồ thị có y = 9 thì ứng với x = 3.
Vậy khi diện tích hình chữ nhật bằng 9 (m2) thì cạnh x = 3 (m)

Ta có : \(f\left(x\right)=x^2+2x+1=\left(x+1\right)^2\)
a, \(f\left(1\right)=\left(1+1\right)^2=2^2=4\)
\(f\left(0\right)=\left(0+1\right)^2=1^2=1\)
b, Ta có : y = 1 hay \(f\left(x\right)=1\)
\(\Leftrightarrow\left(x+1\right)^2=1\Leftrightarrow x^2+2x+1=1\)
\(\Leftrightarrow x^2+2x=0\Leftrightarrow x\left(x+2\right)=0\Leftrightarrow x=0;-2\)
Vậy \(x=\left\{0;-2\right\}\)