Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
- Đường thẳng d’ song song với d nên có dạng: 3x+ y+ m= 0
- IH là khoảng cách từ I đến d’:
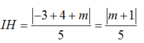
- Xét tam giác vuông IHB:

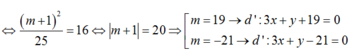

Đáp án D
Trong các dây của đường tròn; dây lớn nhất là đường kính. Nên để d cắt (C) theo 1 dây cung dài nhất thì d phải đi qua tâm I ( -2; 3) của đường tròn.
Vậy d qua I và A(3;2) nên có VTCP ![]() và có VTPT
và có VTPT ![]()
=> phương trình d: 1( x- 3) + 5( y- 2) = 0 hay x+ 5y – 13= 0
Do đó d: x+ 5y -13= 0 .

(C): x 2 + y 2 − 4 x + 2 y − 15 = 0 và đường thẳng ∆: - 4x + 3y + 1 = 0.
Đường tròn (C): x 2 + y 2 − 4 x + 2 y − 15 = 0 có tâm I(2; -1) và bán kính R = 20 .
Khoảng cách d I , ∆ = − 4.2 + 3. − 1 + 1 5 = 2 < R nên đường thẳng cắt đường tròn tại hai điểm phân biệt A, B cách nhau một khoảng là
A B = 2 R 2 − d I , ∆ 2 = 8 .
ĐÁP ÁN C

Đường tròn đã cho có tâm I( - 4; -3).
Để đường thẳng ∆ cắt đường tròn theo dây cung dài nhất thì điểm I nằm trên ∆.
Suy ra: 3. (-4) – 4. (-3) + m = 0
⇔ − 12 + 12 + m = 0 ⇔ m = 0
Đáp án A

Đáp án A
- Từ giả thiết : đường tròn (C1) tâm I(0;0); R = 13 đường tròn (C2) tâm J( 6;0) và R’= 5
- Gọi đường thẳng d qua A có véc tơ chỉ phương:

- d cắt (C1) tại A,B:
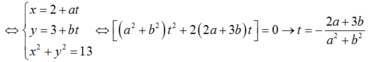
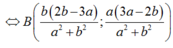
Tương tự d cắt (C2) tại A; C thì tọa độ của A; C là nghiệm của hệ :
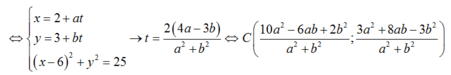
- Nếu 2 dây cung bằng nhau thì A là trung điểm của A; C .Từ đó ta có phương trình :
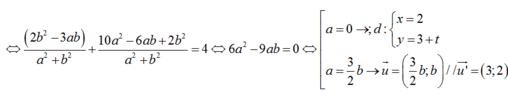
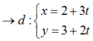
Vậy có 2 đường thẳng: d: x-2 = 0 và d’: 2x -3y + 5= 0.

Đường tròn (C): x 2 + y 2 − 6 x + 8 y − 24 = 0 có tâm I(3; - 4) và bán kính R = 7.
Khoảng cách d I , ∆ = 4.3 + 3. − 4 − m 5 = m 5 .
Để đường thẳng cắt đường tròn theo dây cung có độ dài bằng 10 ta có:
10 = 2 R 2 − d ( I ; Δ ) 2 ⇔ 5 = 49 − m 2 25 ⇔ 25 = 49 − m 2 25 ⇔ m 2 25 = 24 ⇔ m 2 = 600 ⇔ m = ± 10 6
ĐÁP ÁN B

mình ghi nhầm để rồi, (C) : x2 +y2 -2x+4y-4=0
Đường tròn (C) tâm \(I\left(3;-1\right)\) bán kính \(R=2\)
Chắc bạn ghi nhầm đề câu a, tọa độ A như vậy thì A trùng tâm I luôn còn gì? Khi đó mọi đường thẳng d qua A đều cắt đường tròn với dây cung là đường kính \(\Rightarrow\) ko thể xác định d