Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
b) Do \(0< \alpha< \dfrac{\pi}{2}\) nên các giá trị lượng giác của \(\alpha\) đều dương.
Vì vậy:
\(cos\alpha=\sqrt{1-0,6^2}=\dfrac{4}{5}\).
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=0,6:\dfrac{4}{5}=0,75;cot\alpha=1:tan\alpha=\dfrac{4}{3}\).
Do \(\dfrac{\pi}{2}< \alpha< \pi\) nên \(sin\alpha>0;tan\alpha< 0;cot\alpha< 0\).
\(sin\alpha=\sqrt{1-cos^2\alpha}=\dfrac{\sqrt{51}}{10}\).
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{\sqrt{51}}{10}:\left(-0,7\right)=-\dfrac{\sqrt{51}}{7}\).
\(cot\alpha=\dfrac{1}{tan\alpha}=\dfrac{-7}{\sqrt{51}}\).
Do \(\pi< \alpha< \dfrac{3\pi}{2}\) nên \(sin\alpha,cos\alpha< 0;tan\alpha,cot\alpha< 0\).
\(cos\left(\alpha-\dfrac{\pi}{2}\right)=cos\left(\dfrac{\pi}{2}-\alpha\right)=sin\alpha< 0\).
\(sin\left(\dfrac{\pi}{2}+\alpha\right)=cos\alpha< 0\).
\(tan\left(\dfrac{3\pi}{2}-\alpha\right)=tan\left(\dfrac{3\pi}{2}-\alpha-2\pi\right)\)\(=tan\left(-\dfrac{\pi}{2}-\alpha\right)\)\(=-tan\left(\dfrac{\pi}{2}+\alpha\right)=cot\left(\alpha\right)>0\).
\(cot\left(\alpha+\pi\right)=cot\left(\alpha\right)>0\).
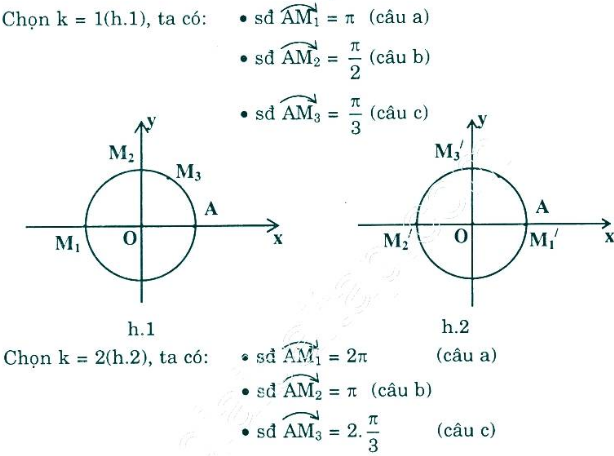
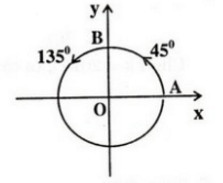
a) Trên hình bên. Cung có số đo 
b) Nhận xét rằng 1350 – ( -2250 ) = 3600 . Như vậy cung 1350 và cung -2250 có chung điểm ngọn. Mà cung 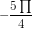cũng là cung -2250 . Vậy cung 1350 cũng chính là cung theo chiều dương
c)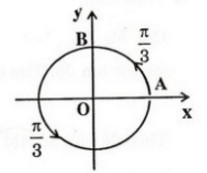 
d)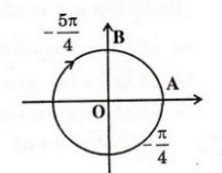 
Có \(a\) thuộc góc phần tư thứ III -> sin\(a\) < 0
+) sin\(a\)=-\(\sqrt{1-cos^2a}\)=-\(\sqrt{1-\left(\dfrac{-12}{13}\right)^2}\)=\(\dfrac{-5}{13}\)
\(cos2a=cos^2a-sin^2a\)=\(\left(\dfrac{-12}{13}\right)^2-\left(\dfrac{-5}{13}\right)^2=\dfrac{119}{169}\)
đề sai nhỉ? sina/2; cos a/2; tana/2; cota/2 chứ?
ta có:
\(sin^2\dfrac{a}{2}=\dfrac{1-cosa}{2}=\dfrac{1-\dfrac{5}{13}}{2}=\dfrac{4}{13}\)
\(\dfrac{3\pi}{2}< a< 2\pi\Leftrightarrow\dfrac{3\pi}{4}< \dfrac{a}{2}< \pi\)
=> sina/2 > 0 => sina/2 = \(\dfrac{2}{\sqrt{13}}\)
ta có:
\(cos^2\left(\dfrac{a}{2}\right)=1-sin^2\left(\dfrac{a}{2}\right)=1-\dfrac{4}{13}=\dfrac{9}{13}\)
\(\dfrac{3\pi}{2}< a< 2\pi\Leftrightarrow\dfrac{3\pi}{4}< \dfrac{a}{2}< \pi\) (cung2)
=> cosa/2 < 0 => cosa/2 = \(\dfrac{-3}{\sqrt{13}}\)
\(tan\left(\dfrac{a}{2}\right)=\dfrac{sin\left(\dfrac{a}{2}\right)}{cos\left(\dfrac{a}{2}\right)}=\dfrac{\dfrac{2}{\sqrt{13}}}{-\dfrac{3}{\sqrt{13}}}=-\dfrac{2}{3}\)
\(cot\left(\dfrac{a}{2}\right)=\dfrac{1}{tan\left(\dfrac{a}{2}\right)}=\dfrac{1}{-\dfrac{2}{3}}=-\dfrac{3}{2}\)
a) Do \(\pi< \alpha< \dfrac{3\pi}{2}\) nên \(sin\alpha< 0;cot\alpha>0;tan\alpha>0\).
Vì vậy: \(sin\alpha=-\sqrt{1-cos^2\alpha}=\dfrac{-\sqrt{15}}{4}\).
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{-\sqrt{15}}{4}:\dfrac{-1}{4}=\sqrt{15}\).
\(cot\alpha=\dfrac{1}{tan\alpha}=\dfrac{1}{\sqrt{15}}\).
b) Do \(\dfrac{\pi}{2}< \alpha< \pi\) nên \(cos\alpha< 0;tan\alpha< 0;cot\alpha< 0\).
\(cos\alpha=-\sqrt{1-sin^2\alpha}=-\dfrac{\sqrt{5}}{3}\);
\(tan\alpha=\dfrac{2}{3}:\dfrac{-\sqrt{5}}{3}=\dfrac{-2}{\sqrt{5}}\); \(cot\alpha=1:tan\alpha=\dfrac{-\sqrt{5}}{2}\).
a) Do 0 < α < nên sinα > 0, tanα > 0, cotα > 0
sinα =
cotα = ; tanα =
b) π < α < nên sinα < 0, cosα < 0, tanα > 0, cotα > 0
cosα = -√(1 - sin2 α) = -√(1 - 0,49) = -√0,51 ≈ -0,7141
tanα ≈ 0,9802; cotα ≈ 1,0202.
c) < α < π nên sinα > 0, cosα < 0, tanα < 0, cotα < 0
cosα = ≈ -0,4229.
sinα =
cotα = -
d) Vì < α < 2π nên sinα < 0, cosα > 0, tanα < 0, cotα < 0
Ta có: tanα =
cosα =