Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Khi x=9 thì A=(9-2)/(3+2)=7/5
b: \(B=\dfrac{x-\sqrt{x}+2\sqrt{x}+2-4}{x-1}=\dfrac{x+\sqrt{x}-2}{x-1}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
c: P=A*B
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\cdot\dfrac{x-2}{\sqrt{x}+2}=\dfrac{x-2}{\sqrt{x}+1}\)
P=7/4
=>(x-2)/(căn x+1)=7/4
=>4x-8=7căn 7+7
=>4x-7căn x-15=0
=>căn x=3(nhận) hoặc căn x=-5/4(loại)
=>x=9

1. \(x=\frac{1}{9}\) thỏa mãn đk: \(x\ge0;x\ne9\)
Thay \(x=\frac{1}{9}\) vào A ta có:
\(A=\frac{\sqrt{\frac{1}{9}}+1}{\sqrt{\frac{1}{9}}-3}=-\frac{1}{2}\)
2. \(B=...\)
\(B=\frac{3\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\frac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\frac{4x+6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(B=\frac{3x-9\sqrt{x}+x+3\sqrt{x}-4x-6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(B=\frac{-6\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
3. \(P=A:B=\frac{\sqrt{x}+1}{\sqrt{x}-3}:\frac{-6\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(P=\frac{\sqrt{x}+3}{-6}\)
Vì \(\sqrt{x}+3\ge3\forall x\)\(\Rightarrow\frac{\sqrt{x}+3}{-6}\le\frac{3}{-6}=-\frac{1}{2}\)
hay \(P\le-\frac{1}{2}\)
Dấu "=" xảy ra <=> x=0

1) Sửa đề: x=0,09
Thay x=0,09 vào A, ta được:
\(A=\dfrac{\sqrt{0.09}}{\sqrt{0.09}-1}=\dfrac{0.3}{0.3-1}=\dfrac{0.3}{-0.7}=\dfrac{-3}{7}\)

1: Khi x=64 thì \(A=\dfrac{8+2}{8}=\dfrac{10}{8}=\dfrac{5}{4}\)
2: \(B=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)+2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-1+2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
3: A/B>3/2
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}}:\dfrac{\sqrt{x}+2}{\sqrt{x}+1}-\dfrac{3}{2}>0\)
=>\(\dfrac{\sqrt{x}+1}{\sqrt{x}}-\dfrac{3}{2}>0\)
=>\(\dfrac{2\sqrt{x}+2-3\sqrt{x}}{\sqrt{x}\cdot2}>0\)
=>\(-\sqrt{x}+2>0\)
=>-căn x>-2
=>căn x<2
=>0<x<4
1) Thay x=64 vào A ta có:
\(A=\dfrac{2+\sqrt{64}}{\sqrt{64}}=\dfrac{2+8}{8}=\dfrac{5}{4}\)
2) \(B=\dfrac{\sqrt{x}-1}{\sqrt{x}}+\dfrac{2\sqrt{x}+1}{x+\sqrt{x}}\)
\(B=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(B=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(B=\dfrac{x-1+2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(B=\dfrac{x+2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(B=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(B=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
3) Ta có:
\(\dfrac{A}{B}>\dfrac{3}{2}\) khi
\(\dfrac{\sqrt{x}+2}{\sqrt{x}}:\dfrac{\sqrt{x}+2}{\sqrt{x}+1}>\dfrac{3}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{x}+2}{\sqrt{x}}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}+2}>\dfrac{3}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}}>\dfrac{3}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}}-\dfrac{3}{2}>0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}+2-3\sqrt{x}}{2\sqrt{x}}>0\)
\(\Leftrightarrow\dfrac{2-\sqrt{x}}{2\sqrt{x}}>0\)
Mà: \(2\sqrt{x}\ge0\forall x\)
\(\Leftrightarrow2-\sqrt{x}>0\)
\(\Leftrightarrow\sqrt{x}< 2\)
\(\Leftrightarrow x< 4\)
Kết hợp với đk:
\(0< x< 4\)

giải phương trình
a)\(\sqrt{x^8}=256\) b)\(\sqrt{x^2-2x+1}=x-1\)

a: TXĐ: D=[0;+\(\infty\))\{1}
\(B=\dfrac{1}{2\sqrt{x}-2}-\dfrac{1}{2\sqrt{x}+2}-\dfrac{\sqrt{x}}{x-1}\)
\(=\dfrac{\sqrt{x}+1-\sqrt{x}+1-2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\cdot2}\)
\(=\dfrac{-1}{\sqrt{x}+1}\)
\(a,ĐK:x\ge0\\ x\ne1\\ B=\dfrac{\sqrt{x}+1-\sqrt{x}+1-2\sqrt{x}}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ B=\dfrac{2\left(1-\sqrt{x}\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{-1}{\sqrt{x}+1}\\ b,x=3\Leftrightarrow B=\dfrac{-1}{\sqrt{3}+1}=\dfrac{1-\sqrt{3}}{2}\\ c,\left|B\right|=\dfrac{1}{2}\Leftrightarrow\left|\dfrac{-1}{\sqrt{x}+1}\right|=\dfrac{1}{2}\\ \Leftrightarrow\dfrac{1}{\sqrt{x}+1}=\dfrac{1}{2}\left(\sqrt{x}+1\ge1>0\right)\\ \Leftrightarrow\sqrt{x}+1=2\Leftrightarrow x=1\left(tm\right)\)



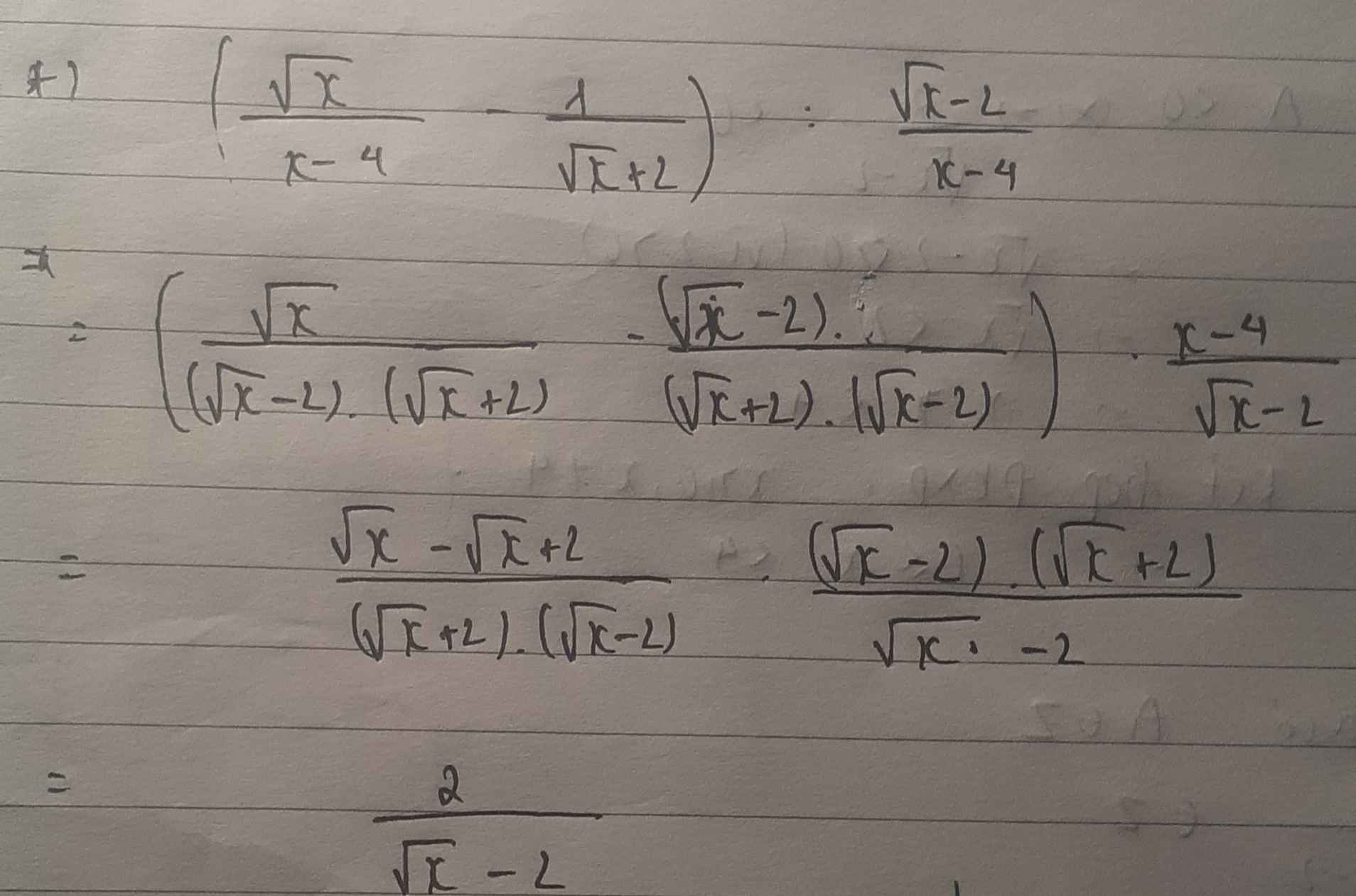


a: \(B=\dfrac{1}{\sqrt{x}-2}-\dfrac{\sqrt{x}}{4-x}\)
\(=\dfrac{1}{\sqrt{x}-2}+\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}+2+\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
Khi x=16 thì \(B=\dfrac{2\cdot4+2}{\left(4-2\right)\left(4+2\right)}=\dfrac{10}{2\cdot6}=\dfrac{10}{12}=\dfrac{5}{6}\)
b: P=B/A
\(=\dfrac{2\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}:\dfrac{2}{\sqrt{x}+2}\)
\(=\dfrac{2\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}+2}{2}=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)
c: P<1
=>P-1<0
=>\(\dfrac{\sqrt{x}+1-\sqrt{x}+2}{\sqrt{x}-2}< 0\)
=>\(\dfrac{3}{\sqrt{x}-2}< 0\)
=>\(\sqrt{x}-2< 0\)
=>\(\sqrt{x}< 2\)
=>0<=x<4
mà x nguyên
nên \(x\in\left\{0;1;2;3\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{0;1;2;3\right\}\)