Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ĐKXĐ: x ≠ 0; x ≠ -1; x ≠ 1/2.
Rút gọn được A = (x - 1)/3
b) Từ 2014 - |2x - 1| = 2013
Tìm được x = 1; x = 0 (loại x = 0 do không thỏa mãn ĐK)
Thay x = 1 vào biểu thức. Tính được A = 0.
c) A< 0 suy luận được x<1 và : x ≠ 0; x ≠ -1; x ≠ 1/2 .
d) Lập luận để khẳng định được x-1 là bội của 3 suy ra , x = 3n+1 (n ∈ Z)

điều kiện: \(x\ne\pm3\)
A = \(\frac{3\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}+\frac{x+3}{\left(x+3\right)\left(x-3\right)}+\frac{18}{\left(x-3\right)\left(x+3\right)}\)
= \(\frac{3x-9+x+3+18}{\left(x-3\right)\left(x+3\right)}=\frac{4\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\)
= \(\frac{4}{x-3}\)
Với x = 1 thì A = \(\frac{4}{1-3}=-2\)
a, ĐKXĐ : x+3 khác 0 ; x-3 khác 0 ; x^2-9 khác 0 <=> x khác -3 và 3
b, A = 3.(x-3)+x+3+18/(x-3).(x+3) = 4x+12/(x+3).(x-3) = 4.(x+3)/(x+3).(x-3) = 4/x-3
c, Khi x =1 thì A = 4/1-3 = -2
k mk nha

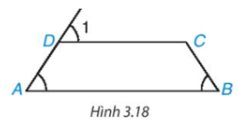
Ta có \(\widehat A = \widehat {{D_1}}\) mà hai góc này ở vị trí đồng vị nên AB // CD.
Suy ra tứ giác ABCD là hình thang.
Mặt khác hình thang ABCD có \(\widehat A = \widehat B\) nên ABCD là hình thang cân.
Do đó AD = BC (đpcm).

Đáp án đúng là: C
Trong Hình 4.31 có \(\widehat {AMN} = \widehat {ABC}\) mà hai góc này ở vị trí đồng vị nên MN // BC.
Áp dụng định lí Thalès vào tam giác ABC, ta có:
\(\dfrac{{AM}}{{BM}} = \dfrac{{AN}}{{CN}}\) hay \(\dfrac{2}{3} = \dfrac{{1,5}}{x}\)
Suy ra \(x = \dfrac{{1,5.3}}{2} = 2,25\)
Vậy x = 2,25.


Sau khi ib với Đinh Lan Anh thì \(P=\frac{2a^2}{a^2-1}+\frac{a}{a+1}-\frac{a}{a-1}\)
\(a,ĐKXĐ:\hept{\begin{cases}a+1\ne0\\a-1\ne0\end{cases}\Leftrightarrow a\ne\pm1}\)
\(b,P=\frac{2a^2}{a^2-1}+\frac{a}{a+1}-\frac{a}{a-1}\)
\(=\frac{2a^2+a\left(a-1\right)-a\left(a+1\right)}{\left(a-1\right)\left(a+1\right)}\)
\(=\frac{2a^2+a^2-a-a^2-q}{\left(a-1\right)\left(a+1\right)}\)
\(=\frac{2a^2-2a}{\left(a-1\right)\left(a+1\right)}\)
\(=\frac{2a\left(a-1\right)}{\left(a-1\right)\left(a+1\right)}\)
\(=\frac{2a}{a+1}\)
\(c,P=\frac{2a}{a+1}=\frac{2a+2}{a+1}-\frac{2}{a+1}=2-\frac{2}{a+1}\)
Để \(P\inℤ\)thì \(2-\frac{2}{a+1}\inℤ\)
\(\Leftrightarrow\frac{2}{a+1}\inℤ\)
Mà \(a\inℤ\Rightarrow a+1\inℤ\)
Ta có bảng
| a + 1 | -2 | -1 | 1 | 2 |
| a | -3 | -2 | 0 | 1 |
Kết hợp ĐKXĐ \(a\ne\pm1\)ta được \(a\in\left\{-3;-2;0\right\}\)
Vậy //////
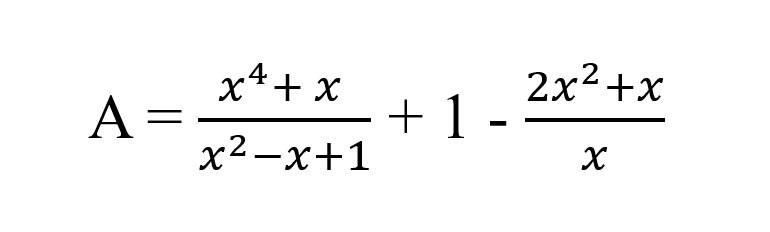






a) \(A=\dfrac{x^4+x}{x^2-x+1}+1-\dfrac{2x^2+x}{x}\)
\(A=\dfrac{x.\left(x^3+1\right)}{x^2-x+1}+1-\dfrac{x.\left(2x+1\right)}{x}\)
\(A=\dfrac{x.\left(x+1\right).\left(x^2-x+1\right)}{x^2-x+1}+1-\left(2x+1\right)\)
\(A=x\left(x+1\right)+1-2x-1\)
\(A=x^2+x-2x=x^2-x\)
b) \(A=6\)
\(\Leftrightarrow x^2-x=6\)
\(\Leftrightarrow x^2-x-6=0\)\(\)
\(\Leftrightarrow\left(x-3\right)\left(x+2\right)=0\)
\(\Leftrightarrow x-3=0\) hay \(x+2=0\)
\(\Leftrightarrow x=3\) hay \(x=-2\)
c) \(A=x^2-x\)
\(A=x^2-x+\dfrac{1}{4}-\dfrac{1}{4}\)
\(A=\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\)
mà \(\left(x-\dfrac{1}{2}\right)^2\ge0\)
\(\Rightarrow A=\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)
\(\Rightarrow Min\left(A\right)=-\dfrac{1}{4}\)