Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: (d)'//(d) nên (d'): y=-3x+b
Thay x=1 và y=2 vào (d'), ta được:
b-3=2
=>b=5
=>y=-3x+5
b: PTHĐGĐ là;
mx^2+3x-1=0
Để (d) cắt (P) tại hai điểm phân biệt nằm về cùng một phía so với trục tung thì
(-3)^2-4*m*(-1)>0 và -1/m>0
=>m<0 và 9+4m>0
=>m<0 và m>-9/4
=>-9/4<m<0

a: 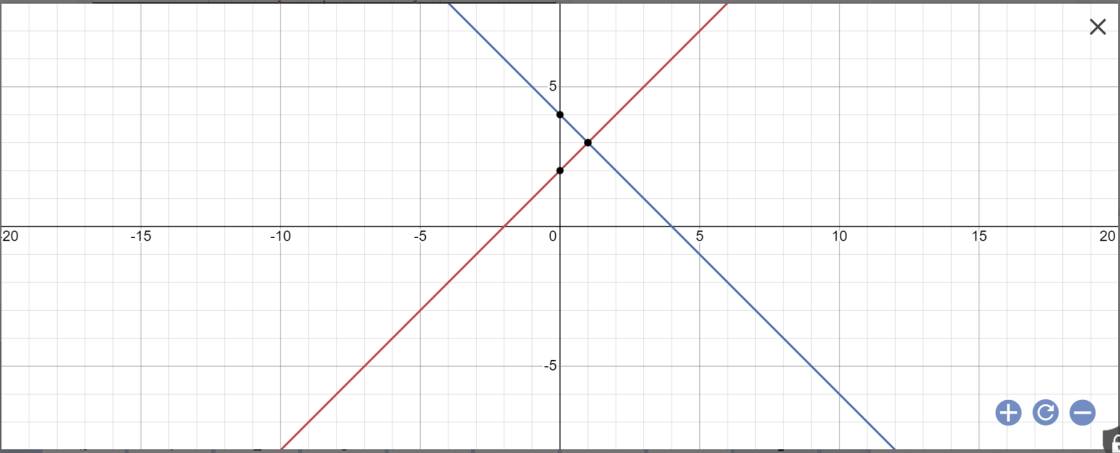
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)
Thay x=1 và y=3 vào (d3), ta được:
\(1\cdot m+m=3\)
=>2m=3
=>\(m=\dfrac{3}{2}\)

Bài 3:
Đặt \(a=m^2-4\)
\(a)\) Đồ thị hàm số \(y=\left(m^2-4\right)x-5\)nghịch biến
\(\Leftrightarrow a< 0\)
\(\Leftrightarrow m^2-4< 0\)
\(\Leftrightarrow m^2< 4\)
\(\Leftrightarrow-\sqrt{4}< m< \sqrt{4}\)
\(\Leftrightarrow-2< m< 2\)
Vậy với \(-2< m< 2\)thì hàm số nghịch biến
\(b)\) Đồ thị hàm số \(y=\left(m^2-4\right)x-5\)đồng biến \(\forall x>0\)
\(\Leftrightarrow a>0\)
\(\Leftrightarrow m^2-4>0\)
\(\Leftrightarrow m^2>4\)
\(\Leftrightarrow\orbr{\begin{cases}m>2\\m< -2\end{cases}}\)
Vậy với \(\orbr{\begin{cases}m>2\\m< -2\end{cases}}\)thì hàm số đồng biến \(\forall x>0\)

1) \(y=mx+1\left(m\ne0\right)\left(1\right)\) hay \(mx-y+1=0\)
Để đồ thị hàm số \(\left(1\right)\) đi qua điểm \(M\left(-1;-1\right)\) khi và chỉ khi
\(m.\left(-1\right)+1=-1\)
\(\Leftrightarrow-m=-2\)
\(\Leftrightarrow m=2\)
Vậy hàm số \(\left(1\right):y=2x+1\)
Bạn tự vẽ đồ thị nhé!
2) \(y=\left(m^2-2\right)x+2m+3\left(d\right)\)
Để \(\left(1\right)//\left(d\right)\) khi và chỉ khi
\(\left\{{}\begin{matrix}m^2-2=2\\2m+3\ne1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2=4\\2m\ne-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\pm2\\m\ne-1\end{matrix}\right.\) \(\Leftrightarrow m=\pm2\) thỏa đề bài
3) Khoảng cách từ gốc O đến đồ thị hàm số \(\left(1\right)\) là:
\(d\left(O;\left(1\right)\right)=\dfrac{m.0-0+1}{\sqrt[]{2^2+1^2}}=\dfrac{2}{\sqrt[]{5}}\)
\(\Leftrightarrow\dfrac{0.m+1}{\sqrt[]{5}}=\dfrac{2}{\sqrt[]{5}}\)
\(\Leftrightarrow0m=1\)
\(\Leftrightarrow m\in\varnothing\)
Vậy không có giá trị nào của m để thỏa mãn đề bài,
Đáp án:
1. Tìm m để đồ thị hàm số (1) đi qua điểm M (−1;−1). Với m tìm được, vẽ đồ thị hàm số (1) trên mặt phẳng tọa độ Oxy
Để đồ thị hàm số (1) đi qua điểm M (−1;−1), ta cần có m(−1)+1=−1. Từ đó ta có m=−2.
Với m=−2, đồ thị hàm số (1) là một đường thẳng có hệ số góc -2 và đi qua điểm M (−1;−1). Ta có thể vẽ đồ thị hàm số như sau:
[Image of the graph of y=-2x+1]
2. Tìm giá trị của m để đồ thị hàm số (1) song song với đường thẳng y (m² - 2) x + 2m+3 =
Hai đường thẳng song song khi hệ số góc của chúng bằng nhau. Do đó, ta có m=m2−2. Từ đó ta có m=2.
3. Tìm m để khoảng cách từ gốc O đến đồ thị hàm số (1) bằng 2 √5
Khoảng cách từ gốc O đến đồ thị hàm số (1) là khoảng cách từ điểm (0;1) đến đường thẳng y=mx+1. Khoảng cách này được tính theo công thức:
d=|m|
Do đó, ta có d=2552=2.
Từ đó, ta có m=2.
Kết luận:
- Giá trị của m để đồ thị hàm số (1) đi qua điểm M (−1;−1) là m=-2.
- Giá trị của m để đồ thị hàm số (1) song song với đường thẳng y (m² - 2) x + 2m+3 = là m=2.
- Giá trị của m để khoảng cách từ gốc O đến đồ thị hàm số (1) bằng 2 √5 là m=2.
Lưu ý:
- Để giải bài toán 1 và 2, ta có thể thay m=-2 vào hàm số (1) và so sánh với tọa độ của điểm M (−1;−1) hoặc tọa độ của một điểm bất kỳ trên đường thẳng y (m² - 2) x + 2m+3 =.
- Để giải bài toán 3, ta có thể sử dụng công thức tính khoảng cách từ một điểm đến một đường thẳng.
chúc bạn học tốt
(P) đi qua M(1;1)
hay M(1;1) thuộc (P)
\(\Leftrightarrow1=m.1^2\Leftrightarrow m=1\)
bạn tự vẽ nhé