Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


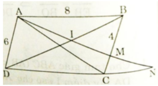
a) AD // BC (gt)![]()
b) Xét ΔAMB và ΔNAD có:
∠BAM = ∠ AND (so le trong, AB // CD)
∠ABM = ∠ADN (góc đối của hình bình hành)
⇒ ΔAMB ∼ ΔNAD (g.g)
c) ΔAMB ∼ ΔNAD (cmt)
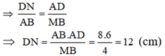
Do đó: CN = DN – DC = 12 – 8 = 4 (cm)
d) Do AB //CD nên theo hệ quả định lí Ta-lét, ta có
![]()
Tương tự, do AD // BM nên
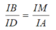
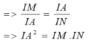

Xét tam giác vuông IBC có:
\(BC^2=IB^2+IC^2\)
\(\Leftrightarrow BC=\sqrt{IB^2+IC^2}=\sqrt{80}\) cm
Vì ABCD là hình chữ nhật
\(\Rightarrow AD=BC=\sqrt{80}\)
Xét tam giác vuông AID có:
\(AD^2=AI^2+ID^2\)
\(\Rightarrow ID8=\sqrt{AD^2-AI^2}=8cm\)

a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của BC
Do đó: EF là đường trung bình
=>EF//AC và EF=AC/2(1)
Xét ΔCDA có
G là trung điểm của CD
H là trung điểm của DA
Do đó: GH là đường trung bình
=>GH//AC và GH=AC/2(2)
Từ (1) và (2) suy ra EF//GH và EF=GH
hay EFGH là hình bình hành
b: EF=GH=AC/2=3(cm)
FG=EH=BD/2=4(cm)

IA=IC=4cm
IB=ID=5cm
\(IA=IC=\dfrac{1}{2}AC=\dfrac{1}{2}.8=4cm\)
\(ID=IB=\dfrac{1}{2}BD=\dfrac{1}{2}.10=5cm\)