Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Kẻ BD vuông góc AC,CE vuông góc AB
góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc AED=góc ACB
=>ΔAED đồng dạng vơi ΔACB
Tâm M của đường tròn ngoại tiếp tứ giác BDCE là trung điểm của BC
Gọi H là giao của BD và CE
=>AH vuông góc BC tại N
Gọi giao của OM với (O) là A'
ΔOBC cân tại O
=>OM vuông góc BC
AN<=A'M ko đổi
=>\(S_{ABC}=\dfrac{1}{2}\cdot AN\cdot BC< =\dfrac{1}{2}\cdot A'M\cdot BC_{kođổi}\)
Dấu = xảy ra khi A trùng A'
=>A là điểm chính giữa của cung BC

Ta giải như sau :
a) 1. Góc ACF + Góc BAC = 90 độ ; Góc EBA + BAC = 90 độ => Góc ACF = Góc EBA (cùng phu với Góc BAC)
Mà ACF và EBA là hai góc chắn cung EF của tứ giác EFBC và bằng nhau
=> Tứ giác EFBC nội tiếp.
2. Ta có : BE vuông góc với AC tại E ; CK vuông góc với AC tại C (Vì góc ACK chắn nửa cung tròn đường kính AK)
=> BE // CK (1)
Tương tự ta cũng có : BK // CF (2)
Từ (1) và (2) suy ra tứ giác BHCK là hình bình hành (dhnb)
b) Vì tứ giác BHCK là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Mà M là trung điểm của BC => M cũng là trung điểm HK
Xét tam giác AHK có AM và HO lần lượt là hai đường trung tuyến ( AO = OK ; HM = MK) cắt nhau tại I
=> I là trọng tâm tam giác AHK
Lại có AM là đường trung tuyến tam giác ABC và I thuộc AM => I là trọng tâm tam giác ABC
c) Mình chưa nghĩ ra :))
giải như sau :
a) 1. Góc ACF + Góc BAC = 90 độ ; Góc EBA + BAC = 90 độ => Góc ACF = Góc EBA (cùng phu với Góc BAC)
Mà ACF và EBA là hai góc chắn cung EF của tứ giác EFBC và bằng nhau
=> Tứ giác EFBC nội tiếp.
2. Ta có : BE vuông góc với AC tại E ; CK vuông góc với AC tại C (Vì góc ACK chắn nửa cung tròn đường kính AK)
=> BE // CK (1)
Tương tự ta cũng có : BK // CF (2)
Từ (1) và (2) suy ra tứ giác BHCK là hình bình hành (dhnb)
b) Vì tứ giác BHCK là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Mà M là trung điểm của BC => M cũng là trung điểm HK
Xét tam giác AHK có AM và HO lần lượt là hai đường trung tuyến ( AO = OK ; HM = MK) cắt nhau tại I
=> I là trọng tâm tam giác AHK
Lại có AM là đường trung tuyến tam giác ABC và I thuộc AM => I là trọng tâm tam giác ABC

S A B C = . AB. AC ≤ 1 2 . A B 2 + A C 2 2 = 1 4 . A B 2 + A C 2
Áp dụng định lý Py-ta-go cho ABC vuông tại A ta có:
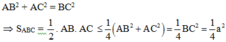
Dấu “=” xảy ra AC = AB => ∆ ABC vuông cân
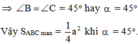
Đáp án cần chọn là: D

Gọi AM là đường trung tuyến kẻ từ A xuống cạnh BC ( M thuộc BC)
Ta có : \(S_{ABC}=\frac{1}{2}BC.AH\)
Vì BC cố định (tức là có độ dài không đổi) nên diện tích tam giác ABC đạt giá trị lớn nhất khi AH đạt giá trị lớn nhất.
Mặt khác, ta luôn có \(AH\le AM=\frac{1}{2}BC\) (hằng số)
Vậy AH đạt giá trị lớn nhất bằng \(AM=\frac{BC}{2}\)
Khi đó diện tích lớn nhất của tam giác ABC là \(S_{ABC}=\frac{1}{2}.BC.\frac{BC}{2}=\frac{BC^2}{4}\)
Vậy khi H trùng với điểm M thì tam giác ABC có diện tích lớn nhất, tức là tam giác ABC vuông cân tại A.