Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a) Vì \(0 - 2.0 + 6 = 6 > 0\) nên (0;0) là một nghiệm của bất phương trình đã cho.
b) Vì \(0 - 2.1 + 6 = 4 > 0\) nên (0;1) là một nghiệm của bất phương trình đã cho.
Vì \(1 - 2.0 + 6 = 7 > 0\) nên (1;0) là một nghiệm của bất phương trình đã cho.
Vì \(1 - 2.1 + 6 = 5 > 0\) nên (1;1) là một nghiệm của bất phương trình đã cho.
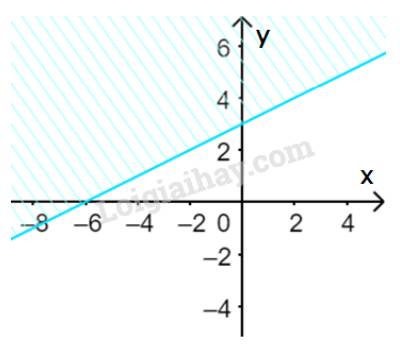
c) Vẽ đường thẳng \(\Delta :x - 2y + 6 = 0\) đi qua hai điểm \(A(0;3)\) và \(B\left( { - 2;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 - 2.0 + 6 = 6 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)

a) Hai bất phương trình bài cho là bất phương trình bậc nhất hai ẩn.
b) (1; 1) là một nghiệm chung của hai BPT (1) và (2) vì:
Thay x=1;y=1 vào (1) ta được: 1-1<3 (Luôn đúng)
Thay x=1; y=1 vào (2) ta được: 1+2.1>-2 (Luôn đúng)

Bước 1: Mở trang Geoebra
Bước 2: Nhập bất phương trình \(x - 2y + 3 \le 0\) vào ô

Và bấm enter, màn hình sẽ hiển thị như hình dưới. Miền nghiệm của bất phương trình \(x - 2y + 3 \le 0\) là miền được tô màu. Đường nét liền biểu thị miền nghiệm chứa các điểm nằm trên đường thẳng \(x - 2y + 3 = 0\).
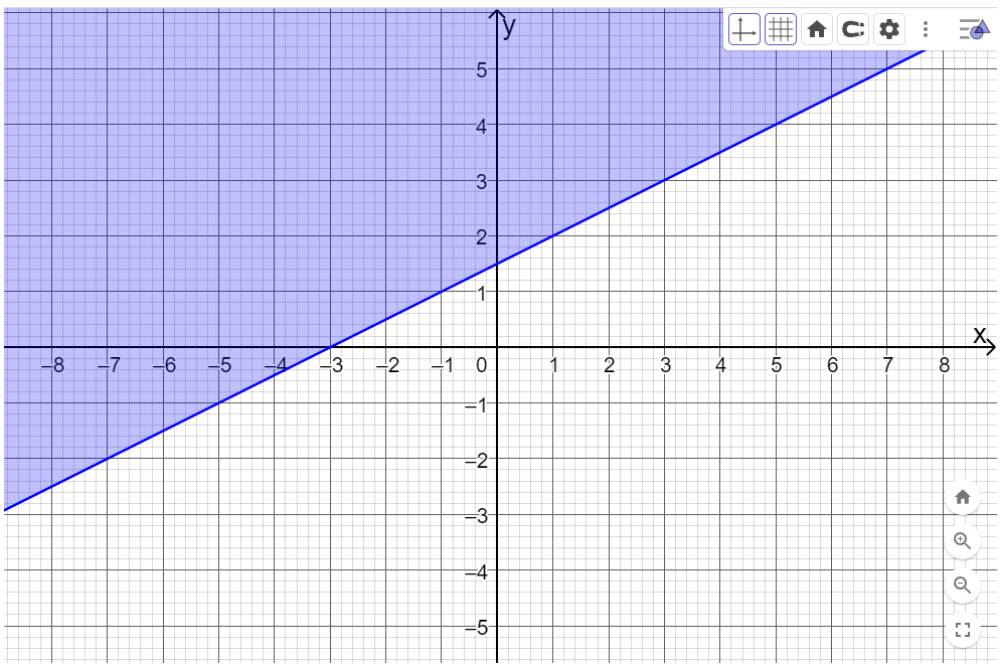
Bước 3: Tiếp tục nhập từng bất phương trình còn lại như sau:
x+3y>-2; \(x \le 0\)(x<=0). Khi đó màn hình sẽ hiển thị như hình dưới.
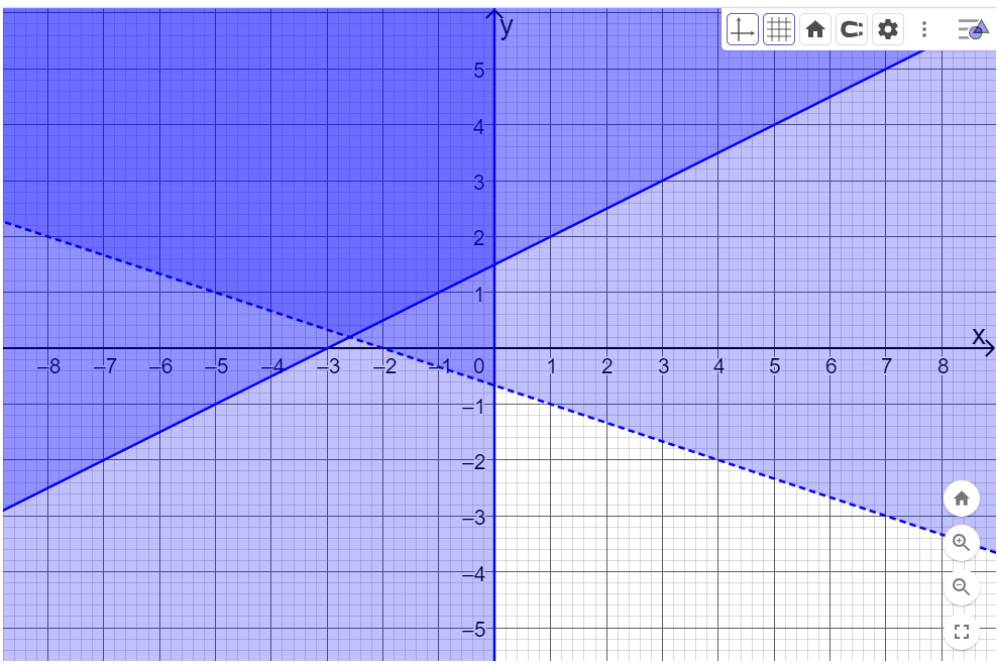
Miền nghiệm của hệ là miền được tô màu đậm nhất. Đường nét đứt biểu thị miền nghiệm không chứa các điểm nằm trên đường thẳng \(x + 3y = - 2\). Đường nét liền \(x = 0\) (trục Oy) biểu thị các điểm nằm trên trục Oy cũng thuộc miền nghiệm.

a) \(5x + 3y < 20\)
Đây là bất phương trình bậc nhất hai ẩn.
Chọn \(x = 0;y = 0\)
Khi đó bất phương trình tương đương với 5.0+3.0
Vậy (0;0) là một nghiệm của bất phương trình trên.
b) \(3x - \frac{5}{y} > 2\)
Đây không là bất phương trình bậc nhất hai ẩn vì có ẩn y ở mẫu.

+ Biểu diễn miền nghiệm của BPT \(x - y \le 6\)
Bước 1: Vẽ đường thẳng \(d:x - y = 6\) trên mặt phẳng tọa độ Õy
Bước 2: Lấy O(0;0) không thuộc d, ta có: \(0 - 0 = 0 \le 6\) => điểm O(0;0) thuộc miền nghiệm
=> Miền nghiệm của BPT \(x - y \le 6\) là nửa mp bờ d, chứa gốc tọa độ.
+ Tương tự, ta có miền nghiệm của BPT \(2x - y \le 2\) là nửa mp bờ \(d':2x - y = 0\), chứa gốc tọa độ.
+ Miền nghiệm của BPT \(x \ge 0\) là nửa mp bên phải Oy (tính cả trục Oy)
+ Miền nghiệm của BPT \(y \ge 0\) là nửa mp phía trên Ox (tính cả trục Ox)
Biểu diễn trên cùng một mặt phẳng tọa độ và gạch bỏ các miền không là nghiệm của từng BPT, ta được:
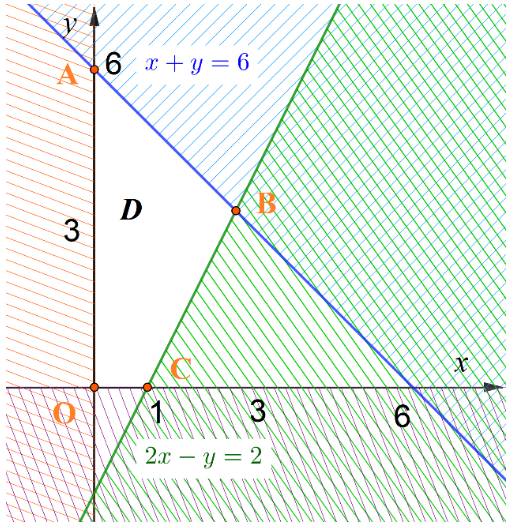
Miền nghiệm của hệ bất phương trình đã cho là miền tứ giác OABC (miền không bị gạch) với \(A(0;6),B(\frac{8}{3};\frac{{10}}{3}),C(1;0)\)
b)
Thay tọa độ các điểm \(O(0;0),A(0;6),B(\frac{8}{3};\frac{{10}}{3}),C(1;0)\) và biểu thức \(F(x;y) = 2x + 3y\) ta được:
\(\begin{array}{l}F(0;0) = 2.0 + 3.0 = 0\\F(0;6) = 2.0 + 3.6 = 18\\F(\frac{8}{3};\frac{{10}}{3}) = 2.\frac{8}{3} + 3.\frac{{10}}{3} = \frac{{46}}{3}\\F(1;0) = 2.1 + 3.0 = 2\end{array}\)
\( \Rightarrow \min F = 0\), \(\max F = 18\)
Vậy trên miền D, giá trị nhỏ nhất của F bằng 0, giá trị lớn nhất của F bằng \(18\).

a) \({x^2} + x - 6 \le 0\) là một bất phương trình bậc hai một ẩn
Vì \({2^2} + 2 - 6 = 0\) nên \(x = 2\) là nghiệm của bất phương trình trên
b) \(x + 2 > 0\) không là bất phương trình bậc hai một ẩn
c) \( - 6{x^2} - 7x + 5 > 0\) là một bất phương trình bậc hai một ẩn
Vì \( - {6.2^2} - 7.2 + 5 = - 33 < 0\) nên \(x = 2\) không là nghiệm của bất phương trình trên

Ta thấy hệ \(\left\{ \begin{array}{l}x - y < 0\\2y \ge 0\end{array} \right.\) là hệ bất phương trình bậc nhất hai ẩn với các bất phương trình bậc nhất hai ẩn là \(x - y < 0;2y \ge 0\).
=> Chọn A.
Đáp án B loại vì \(3x + {y^3} < 0\) chứa \(y^3\).
Đáp án C loại vì \({y^2} + 3 < 0\) chứa \(y^2\).
Đáp án D loại vì \( - {x^3} + y < 4\) chứa \(x^3\).
a)
+) Thay x=0 và y=0 vào bất phương trình \(x + 2y \ge 0\), ta được:
\(0 + 2.0 \ge 0 \Leftrightarrow 0 \ge 0\)(Đúng)
=> (0;0) là một nghiệm của bất phương trình \(x + 2y \ge 0\)
+) Thay x=1, y=1 vào bất phương trình \(x + 2y \ge 0\) ta được:
\(1 + 2.1 \ge 0 \Leftrightarrow 3 \ge 0\)(Đúng)
=> (1;1) là một nghiệm của bất phương trình \(x + 2y \ge 0\)
Ta tìm được 2 nghiệm của bất phương trình đã cho là (0;0) và (1;1).
b)
Thay y=0 vào bất phương trình \(x + 2y \ge 0\) ta được:
\(x + 2.0 \ge 0 \Leftrightarrow x \ge 0\)
Ta thấy bất phương trình bài cho tương đương với bất phương trình nên số giá trị của x thỏa mãn bất phương trình đã cho là số x thỏa mãn điều kiện .
Mà ta có vô số giá trị của x thỏa mãn nên có vô số giá trị của x thỏa mãn bất phương trình đã cho.
Chú ý
Ta có thể thử các cặp số khác đối với câu a, miễn là cặp số đấy làm cho bất phương trình đúng.