Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

• Ta có:
- Số trung bình cộng x = 55,82 trường là không có nghĩa.
- Trong các số liệu thống kê đã cho có sự chênh lệch quá lớn (điều này chứng tỏ các số liệu thống kê đã cho là không cùng loại)
Chỉ cần một trong hai điều kể trên là đủ để suy ra rằng: Không chọn được số trung bình cộng làm đại diện cho các số liệu thống kê.
• Dễ thấy: Bảng số liệu thống kê đã cho không có mốt.
• Trong trường hợp đã cho, ta chọn số trung vị M e = 40 (trường) để làm đại diện cho các số liệu thống kê đã cho (về quy mô và độ lớn).
Đáp án: B

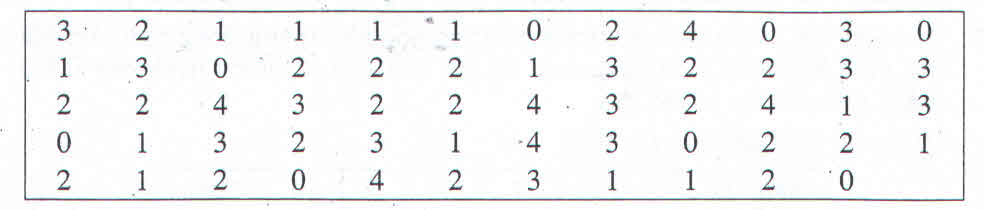
a) Bảng phân bố tần số và tần suất:
| Số con | Tần số | Tần suất |
| 0 | 8 | 13,6% |
| 1 | 13 | 22% |
| 2 | 19 | 32,2% |
| 3 | 13 | 22% |
| 4 | 6 | 10,2% |
| Cộng | 59 | 100% |
b) Nhận xét: Hầu hết các gia đình có từ 1 đến 3 con.
Số gia đình có 2 con là nhiều nhất.
c) Số trung bình cộng:
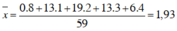
Mốt: M0 = 2 (có tần số lớn nhất bằng 19).
Sắp xếp dãy số liệu theo thứ tự không giảm:
0; 0; 0; …; 0; 1; 1; ….; 1; 2; 2; …; 2; 3; 3; …; 3; 4; 4; …; 4
Có 59 số liệu nên số trung vị là số thứ 30 trong dãy trên.
Số thứ 30 là 2 nên số trung vị Me = 2.

*) Sắp xếp thứ tự của mẫu số liệu theo thứ tự không giảm ta được: 1 2 4 5 9 10 11
a) Số trung bình cộng của mẫu số liệu trên là: \(\overline x = \frac{{1{\rm{ + }}2{\rm{ + }}4{\rm{ + }}5{\rm{ + }}9{\rm{ + }}10{\rm{ + }}11}}{7} = 6\)
b) Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 7 số liệu ( lẻ ) nên trung vị \({Q_2} = 5\)
c) Tứ phân vị của mẫu số liệu trên là:
Trung vị của dãy 1, 2, 4 là: \({Q_1} = 2\)
Trung vị của dãy 9, 10, 11 là: \({Q_3} = 10\)
Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 2\), \({Q_2} = 5\), \({Q_3} = 10\)
d) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 11 - 1 = 10\)
e) Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 10 - 2 = 8\)
g) Phương sai của mẫu số liệu trên là: \({s^2} = \frac{{\left[ {{{\left( {1 - \overline x } \right)}^2} + {{\left( {2 - \overline x } \right)}^2} + ... + {{\left( {11 - \overline x } \right)}^2}} \right]}}{7} = \frac{{96}}{7}\)
h) Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} = \sqrt {\frac{{96}}{7}} \)

Chọn A.
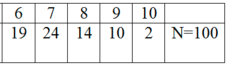
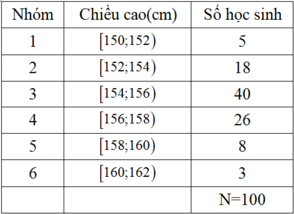
Để tính số trung bình ta xác định thêm cột giá trị đại diện của mỗi lớp
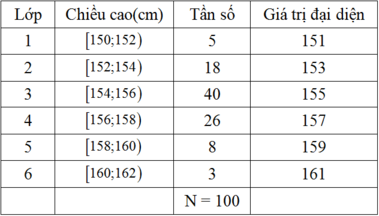
Trung bình cộng của bảng số liệu là:
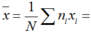
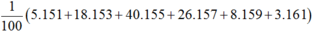

a) Bảng phân bố tần số và tần suất
|
Số con trong một hộ |
Tần số |
Tần suất (%)
|
|
0 1 2 3 4 |
8 13 19 13 6 |
0,14 0,22 0,32 0,22 0,1 |
|
Cộng |
59 |
100% |
b) Nhận xét: Số hộ có 1 và 2 và 3 con chiếm tỉ lệ xấp xỉ 90%. Số hộ có 2 con chiếm tỉ lệ cao nhất 32%.
c) Số trung bình: = 159159(15.1+22.2+16.3+6.4) ≈ 2,22
Số mốt M0 = 2 (con)
Số trung vị Me = 2

a) Ta có: \(8 - 7 = 1;6 - 7 = - 1;7 - 7 = 0;5 - 7 = - 2;9 - 7 = 2\)
b) +) Bình phương các độ lệch là: \({(8 - 7)^2} = 1;{(6 - 7)^2} = 1;{(7 - 7)^2} = 0;{(5 - 7)^2} = 4;{(9 - 7)^2} = 4\)
+) Trung bình cộng của bình phương các độ lệch là:
\({s^2} = \frac{{{{(8 - 7)}^2} + {{(6 - 7)}^2} + {{(7 - 7)}^2} + {{(5 - 7)}^2} + {{(9 - 7)}^2}}}{5} = 2\)

Điểm số của xạ thủ A có:
x ≈ 8 , 3 đ i ể m , s 1 2 ≈ 1 , 6 ; s 1 ≈ 1 , 27 .
Điểm số của xạ thủ B có
y ≈ 8 , 4 đ i ể m , s 2 2 ≈ 1 , 77 ; s 2 ≈ 1 , 27 .

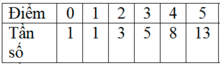
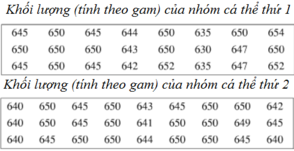
a) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
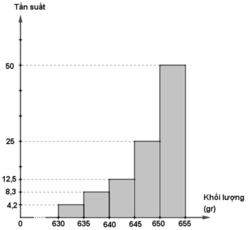
| [630;635) | 1 | 4,2% |
| [635;640) | 2 | 8,3% |
| [640;645) | 3 | 12,5% |
| [645;650) | 6 | 25% |
| [650;655] | 12 | 50% |
| Cộng | 24 | 100% |
b) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
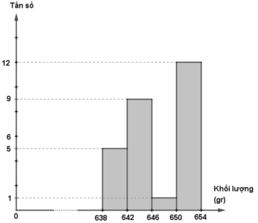
| [638;642) | 5 | 18,52% |
| [642;646) | 9 | 33,33% |
| [646;650) | 1 | 3,7% |
| [650;654) | 12 | 44,45% |
| Cộng | 27 | 100% |
c) Biểu đồ tần suất hình cột:
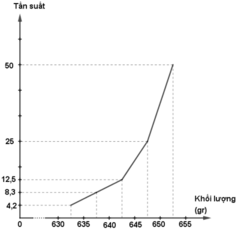
- Đường gấp khúc tần suất
d) Biểu đồ tần số
- Đường gấp khúc tần số
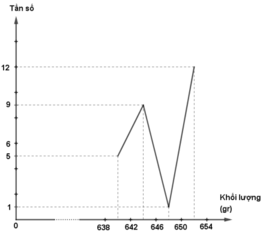
e) * Xét bảng phân bố ở câu a)
- Số trung bình:
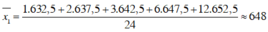
- Phương sai:
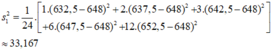
- Độ lệch chuẩn:
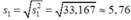
* Xét bảng phân bố ở câu b):
- Số trung bình:
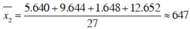
- Phương sai:
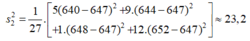
- Độ lệch chuẩn:
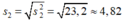
Nhận thấy s2 < s1 nên nhóm cá thứ hai có khối lượng đồng đều hơn.




Chọn D.
Số trung bình cộng là: